|
(28)兵庫県 | 学習日 月 日( ) |
|
(28)兵庫県 | 学習日 月 日( ) |
| 1 | 〜 2番問題 (おまけ) 〜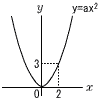 図のように,関数 y=ax2 のグラフ上に点(2,3)がある。 図のように,関数 y=ax2 のグラフ上に点(2,3)がある。次の問いに答えなさい。 |
||||||
| 2 |
|
||||||
| 3 | √50+√8 |
1 | aの値を求めなさい。 |
||||
| 4 | (a+b)2−16 を因数分解しなさい。 |
2 | 次の[ア]と[イ]にあてはまる数をそれぞれ求めなさい。 関数 y=ax2 において,xの変域が b≦x≦2 のときの yの変域は 0≦y≦3 である。 このとき,bの範囲は [ア]≦b≦[イ] である。 |
||||
| 5 | 2次方程式 x2−5x−1=0 を解きなさい。 |
||||||
| 6 |
|
3 | 関数 y=ax2 において,xの変域が −4≦x≦3 のときのyの変域と,関数 y=cx2 において,xの変域が −2≦x≦3 のときのyの変域とが等しいとき,cの値を求めなさい。 |
||||
| 7 | 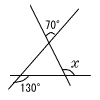 図のように,3つの直線が交わっている。∠xの大きさは何度か,求めなさい。 図のように,3つの直線が交わっている。∠xの大きさは何度か,求めなさい。 |
||||||
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] [答のペ−ジに進む] |