| 【 前 期 】 |
【 中 期 】 |
| 1 |
 9×(−5)+(−2)3 9×(−5)+(−2)3
|
1 |
 |
6÷(− |
2 |
)+(−5)2 |
| 3 |
|
| 2 |
|
2 |
(2x−7)(2x+7)+(x+4)2
|
| 3 |
次のア〜ウを,値の小さいものから順に記号で書け。
ア 7 イ 5√2 ウ 4√3
|
3 |
√30÷√5−√42×√7
|
| 4 |
半径が9cmの球の表面積を求めよ。ただし,円周率はπとする。
|
4 |
2x2+4x−48 を因数分解せよ。
|
| 5 |
次の連立方程式を解け。
|
5 |
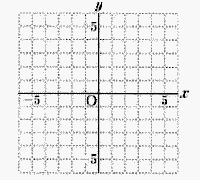 一次関数 一次関数
のグラフをかけ。
|
| 6 |
312−292
|
6 |
二次方程式 x2+3x−2=0 を解け。
|
| 7 |
yはxの2乗に比例し,x=3のときy=−3である。x=6のときのyの値を求めよ。
|
7 |
500円で,1本a円の鉛筆3本と1冊b円のノート2冊を買うと,おつりがもらえた。このときの数量の関係を表した不等式として適当でないものを,次のア〜エから1つ選べ。
ア 3a+2b<500 イ 500−3a>2b
ウ 500−(3a+2b)>0 エ 500−2b<3a |
| 8 |
xについての方程式 3x−10+a2=0 の解がx=−2であるとき,aの値を求めよ。
|
8 |
次の表は,魚釣りをしていた50人に対して,釣れた魚の数(匹)を調査し,まとめたものである。この調査結果から,釣れた魚の数の中央値(メジアン)と最頻値(モード)を,それぞれ求めよ。
| 釣れた魚の数(匹) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
計 |
| 人 数 (人) |
0 |
4 |
8 |
6 |
2 |
4 |
5 |
6 |
6 |
6 |
3 |
50 |
|
| 9 |
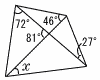 次の図で,∠xの大きさを求めよ。 次の図で,∠xの大きさを求めよ。
|
 一次関数
一次関数 次の図で,∠xの大きさを求めよ。
次の図で,∠xの大きさを求めよ。