全国公立高校入試 　１番問題　【平成２８年春】

（21）岐阜県

学習日　　　 月　　 　日（　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１	7−32	〜　２番問題　（おまけ） 〜 距離(m) 人数(人) 　以上　未満 5　〜　10 １ 10　〜　15 ア 15　〜　20 イ 20　〜　25 ９ 25　〜　30 ６ 30　〜　35  ２ 合計 ３０ 　ある中学校で生徒30人のハンドボール投げの記録を調べた。図は調べた記録を小さいほうから順に並べて書いた用紙の一部であり，表は調べた30人の記録を度数分布表に整理したものである。 　　　　　　　　図 ハンドボール投げの記録（ｍ） 　8　　　11　　　13　　　14　　　14　 　15　　15　　　16　　　17　　　18　 　18　　19　　　19　　　20　　　21
２	4a＋5b−3(a＋2b)
３	√6×√3＋√6÷√3
４	関数 y＝−x2 で，xの値が1から3まで増加するときの変化の割合を求めなさい。	１	表中のア，イにあてはまる数を書きなさい。
５	下の図は，底面の対角線の長さが4cm， 高さが3cmの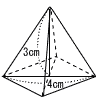正四角すいである。この正四角すいの体積を求めなさい。	２	表から，最頻値を求めなさい。
６	6台の機械で50分間かかる作業がある。この作業を6台の機械で同時に始めた。作業を始めてから35分後に1台の機械が故障したため，残りの作業を5台の機械で続けて行い，作業を終えた。1台の機械が故障してから何分後に作業を終えたかを求めなさい。 　ただし，6台の機械はすべて同じ性能で，途中で故障したのは1台のみとする。	３	25m以上投げた生徒の相対度数を，四捨五入して小数第2位まで求めなさい。