| 1 |
(1)  2+(−4) 2+(−4)
|
5 |
2つのさいころを同時に投げるとき,5の目がまったく出ない確率を求めなさい。
|
(2)  |
62÷ |
4 |
| 3 |
|
(3)  5x−8y−2(2x−3y) 5x−8y−2(2x−3y)
|
6 |
等しい角の作図について考える。
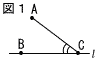 (1) 図1のように,点B,Cは直線l 上にある。 (1) 図1のように,点B,Cは直線l 上にある。
∠ACB=∠A’CBとなる点イを,直線l について点Aの反対側に,次のア,イで作図した。
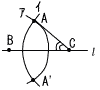 〔作図〕 〔作図〕
ア 点Bを中心として,半径BAの円をかく。
イ 点Cを中心として,半径CAの円をかき,2円の交点の1つをA’とする。
〔説明〕
この作図において,点Bから点A,A’までの距離は等しく,点Cから点A,A’までの距離も等しい。また,BCは共通な辺だから,△ABC≡△A’BCとなる。 |
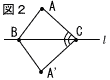 作図した点A’について,説明から,△ABC≡△A’BCなので,図2のように∠ACB=∠ACBがいえる。 作図した点A’について,説明から,△ABC≡△A’BCなので,図2のように∠ACB=∠ACBがいえる。
説明で,根拠として使っている三角形の合同条件を書きなさい。
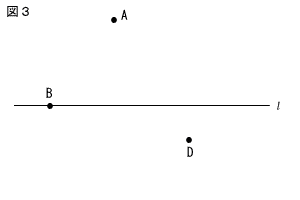
(2) 図3のように,点Dは,直線l について点Aの反対側にある。
直線l 上にあり,∠AEB=∠DEBとなる点Eを,定規とコンパスを用いて作図しなさい。ただし,点Eを表す文字Eも書き,作図に用いた線は消さないこと。
|
(4) (√5−3)(√5+3)
|
| 2 |
10より小さい素数は何個あるか,求めなさい。
|
| 3 |
一次方程式 3x+3=17 を次のように解いた。
3x+3=17 ・・・ (1)
3x=17−3 ・・・ (2)
3x=14 ・・・ (3)
|
上の式(1)から式(2)へ,式(3)から式(4)へ変形してよい理由として正しいものを,次のア〜エから1つづつ選び,記号で書きなさい。
ア
|
等式の両辺に3をたしても等式は成り立つから,変形してよい。 |
イ
|
等式の両辺から3をひいても等式は成り立つから,変形してよい。 |
ウ
|
等式の両辺に3をかけても等式は成り立つから,変形してよい。 |
エ
|
等式の両辺に3でわっても等式は成り立つから,変形してよい。 |
|
| 4 |
二次方程式 x2+7x+9=0 を解きなさい。
|
 |
 (1) 図1のように,点B,Cは直線l 上にある。
(1) 図1のように,点B,Cは直線l 上にある。 作図した点A’について,説明から,△ABC≡△A’BCなので,図2のように∠ACB=∠ACBがいえる。
作図した点A’について,説明から,△ABC≡△A’BCなので,図2のように∠ACB=∠ACBがいえる。