| １ 番 問 題 |
２番問題 （おまけ） |
| １ |
(1)  7−4×(−2)
|
１ |
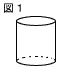  図１の立体は，側面積が100cm2の円柱である。この円柱の底面の円の半径をxcm， 高さをycmとするとき，yをxの式で表しなさい。ただし。円周率はπとする。
また，次のア〜エの中から，xとyの関係について正しく述べたものを1つ選び，記号で答えなさい。
| ア |
yはxの関数であり，.yはxに比例する。 |
| イ |
yはxの関数であり，.yはxに反比例する。 |
ウ
|
yはxの関数であるが，xとyの関係は，比例，反比例のいずれでもない。 |
| エ |
yはxの関数ではない。 |
|
(2) (48a2−18ab)÷6a
|
|
２ |
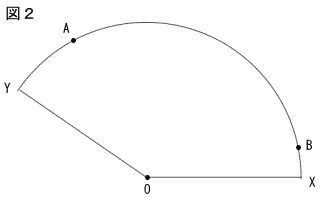
図2において，2点Ａ，Ｂは，おうぎ形ＯＸＹの弧上の点である。次の□の中に示した条件アと条件イの両方に当てはまる点Ｐを作図しなさい。
条件ア 直線ＡＰは，点Ａを接点とする接線である。
条件イ ＡＰ＝ＢＰである。 |
ただし，作図には定規とコンパスを使用し，作図に用いた線は残しておくこと。
|
|
| ２ |
(a−3)(a−8)−a(a＋10) の式の値を求めなさい。
|
３ |
袋の中に，赤玉2個，青玉2個，白玉1個の合計5個の玉が入っている。この袋iの中から，次の□の中に示したAの方法とBの方法で，玉を取り出す。
A
|
1個取り出し，それをもとにもどさずに，続けてもう1個取り出す。 |
B
|
1個取り出し，色を調べて袋の中にもどしてから，もう一度，1個取り出す。 |
|
取り出した2個の玉がともに赤玉であるのは，Ａの方法とＢの方法とでは，どちらが起こりやすいか。それぞれの確率を求め，記号で答えなさい。ただし，袋の中から玉を取り出すとき，どの玉が取り出されることも同様に確からしいものとする。
|
| ３ |
次の２次方程式を解きなさい。
(x＋1)2＝64
|
