| 1 |
(1)  4−9 4−9
|
3 |
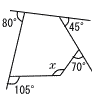
 右の図で∠x の大きさを求めなさい。 右の図で∠x の大きさを求めなさい。
|
| (2) |
 |
1− |
6 |
÷(−3) |
| 5 |
|
(3)  (7a+b)−5(a−2b) (7a+b)−5(a−2b)
|
4 |
| 階級 (cm) |
度数(人) |
相対度数 |
| 以上 未満 |
|
|
| 145.0〜150.0 |
2 |
* |
| 150.0〜155.0 |
* |
0.10 |
| 155.0〜160.0 |
* |
[ ] |
| 160.0〜165.0 |
* |
0.30 |
| 165.0〜170.0 |
* |
0.20 |
| 170.0〜175.0 |
* |
0.10 |
| 計 |
40 |
1.00 |
次の表は,ある中学校3年生の40人について,身長を測定し,その結果を度数分布表に表したものである。
次の(1),(2)に答えなさい。
|
(4)  √27−√12+√3 √27−√12+√3
|
(1) 表の[ ]にあてはまる数を求めなさい。
|
(5) (2x+y)2−(x+2y)2
|
(2) 身長が160.0cm以上の生徒は何人いるか,求めなさい。
|
| 2 |
次の方程式を解きなさい。
|
5 |
  1,2,3の数字が1つずつ書かれた3枚のカードがある。この3枚のカードをよくきって1枚取り出し,書かれた数字を調べてもとにもどすことを,3回繰り返す。それぞれ取り出したカードの数字が偶数ならば2点,奇数ならば1点の得点が入るとき,得点の合計が4点となる確率を求めなさい。 1,2,3の数字が1つずつ書かれた3枚のカードがある。この3枚のカードをよくきって1枚取り出し,書かれた数字を調べてもとにもどすことを,3回繰り返す。それぞれ取り出したカードの数字が偶数ならば2点,奇数ならば1点の得点が入るとき,得点の合計が4点となる確率を求めなさい。
ただし,どのカードの取り出し方も同様に確からしいものとする。
|
