全国公立高校入試 　１番問題　【平成２７年春】

（２９）奈良県

学習日　　　 月　 　　日（　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１	(1)　　−7×6	６	階級(℃)  度数(人)  １月  ２月 　以上 未満 -6　〜　-4    9   1 -4　〜　-2  7  4 -2　〜　 0   14  12  0　〜　2  9  5  2　〜　4  9  4  4　〜　6   1  1  6　〜　8   0  1  計  31  28  　右の表は，ある市の１月と２月の毎日の最低気温を度数分布表に整理したものである。表をもとに，最低気温が0℃未満の日数の割合は，１月と２月とでどちらが大きいかを調べたい。そのことを調べるためには何と何を比べるのがよいか。次のア〜オのうち，正しいものを1つ選び，その記号を書け。 ア　１月の平均値と２月の平均値 イ　１月の最頻値(ﾓｰﾄﾞ)と 　　　２月の最頻値(ﾓｰﾄﾞ) ウ　−2℃以上0℃未満の階級における， 　　　１月の相対度数と２月の相対度数 エ　0℃未満の階級における， 　　　１月の度数の合計と２月の度数の合計 オ　0℃未満の階級における，１月の相対 　　　度数の合計と２月の相対度数の合計
	(2)　ab2×8a2÷2ab
	(3)　　5(x＋2y)＋2(−4x＋y)
	(4)　(x＋y)(x−3y)−9xy
２	連立方程式｛ x＋2y＝4  を解け。 3x−5y＝1	７	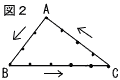ＡＢ＝3cm，BC＝5cm，CA＝4cmの△ABCがある。　図２のように，△ABCの周上に，頂点から1cm間隔で12個の点をとる。2つのさいころを同時に1回投げて出た目の数の和がaのとき，△ＡＢＣの周上にとった12個の点のうち，頂点Ａから左回りにａ番目の位置にある点をＰとする。例えば，aが8のとき，点Ｐは頂点Ｃと一致する。 　2つのさいころを同時に1回投げて，点Ａ，Ｂ，Ｐを結んで直角三角形ができる確率を求めよ。
３	２次方程式 x2−8x＋12＝0 を解け。
４	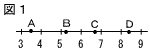図１で，数直線上の4つの点Ａ，Ｂ，Ｃ，Ｄのうち，1つは3√5を表している。　その記号を書け。	８	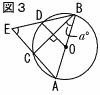図３で，線分ＡＢは円Ｏの直径で，2点Ｃ，Ｄは円Ｏの周上にあり，ＢＣ⊥ＯＤである。また，点Ｅは2直線ＡＣ，ＢＤの交点である。∠ＯＢＣ＝a°のとき，∠ＣＥＤの大きさをaを用いて表せ。
５	yはxに比例し，x＝2のときy＝−6である。x＝−1のときのyの値を求めよ。