全国公立高校入試 　１番問題　【平成２７年春】		正　答　４
		25　滋賀県　〜　32　島根県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

25滋賀県	１　6＋4＝10　　２  6a＋5a ＝  11 a  15  15 ３　4x＋8y−6x−9y＝−2x−y ４   5xy2×7xy ＝35y3  x2 ５　2＋2√2＋1−2√2＝3 ６　もう1つの解をkとすると， 　　　(x＋2)(x−k)＝0 　　　x2＋(2−k)x−2k＝0 もとの方程式x2＋ax−12＝0と係数を比較して 　　　　−2k＝−12だから，k＝6 【別解】 　x2＋ax−12＝0にx＝−2を代入すると， 　　(−2)2＋(−2)a−12＝0 　　4−2a−12＝0より，a＝−4 　よってもとの方程式は，x2−8x−12＝0 　　　(x−6)(x＋2)＝0 　　　　もう1つの解は，x＝6 ７　半球＝  4 π×93×  1 ＝486π  3  2 　求める円錐の高さをhcmとすると 　円錐＝  1 π×92h＝486π  3 　　27πh＝486πより，h＝18cm ８ ア 範囲＝32.5−7.5＝25分（×） イ 最頻値（20人）＝12.5分＜平均値（×） ウ 中央値は25番目で，10〜15分（×） エ 相対度数＝8÷50＝0.16（○） 　　よって正しいのは，エ	29奈良県	１ (1)　−42　　　(2)   ab2×8a2 ＝4a2b   2ab 　(3)　5x＋10y−8x＋2y＝−3x＋12y 　(4)　x2−2xy−3y2−9xy＝x2−11xy−3y2 ２ 上式×3−下式より，11y＝11で，y＝1 　これを上式に代入して，x＋2＝4で，x＝2 　　　よって，x＝2，y＝1 ３　(x−2)(x−6)ー0より，x＝2，6 ４　3√5＝√45で，√36＜√45＜√49 　　　よって，6＜3√5＜7より，Ｃ ５　y＝axに(2,−6)を代入して， 　　　−6＝2aで，a＝−3 　y＝-3xにx＝-1を代入して，y＝-3×(-1)＝3 ６　オ ７　ＰはＡＣ上の点（Ａは除く）だから， 　　a＝8のとき 5通り，a＝9のとき 4通り， 　　a＝10のとき 3通り，a＝11のとき 2通り 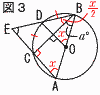　よって，確率＝  5＋4＋3＋2 ＝  14 ＝   7  36  36 18 ８　（右図参照） ∠ＢＯＤ＝∠ＢＡＥ＝xとすると 　弧ＢＤ＝弧ＣＤより， 　　　∠ＣＢＤ＝x/2 　△ＡＢＣで，∠x＝(90−a)° 　∠ＣＥＤ＝90−  x ＝90− 90−a  2  　2　 　　　＝(45＋  a )°   2
26京都府	１ 5×16−9＝80−9＝71 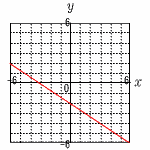２ 　 4(5x−3y)−3(3x−7y) 3×4　 　＝ 20x−12y−9x＋21y ＝ 11x＋9y 12 12 ３ 3√3− 12√3 −5√3＝−6√3  3 ４　与式＝(x＋y)(x−y)＝2√7×4＝8√7 ５　（答は右図） 　　3y＝−2x−6より， 　　y＝−  2 x−2   3 　グラフは，切片−2 　　傾き(−2/3）の直線 【別解】 　x＝0のとき，y＝−2 　y＝0のとき，x＝−3 　　よって，(0,−2)と(−3,0)を通る直線 ６ x−2＝±√6より，x＝2±√6 ７ 6本から2本取り出す方法は，  6×5 ＝15通り 　2  　このうち，和が3の倍数になるのは， 　3，6，9，12，18，24，33，36，48 　　の9通りだから， 　よって，確率＝  9 ＝  3 15  5 ８ 白い玉をx個とすると，  80 . ＝  9 x＋80 50 　9x＋720＝4000より，x＝  3280 ≒364.4   　9　 　　よって，およそ360個で，イ	30和歌山県	１ (1)−5　(2) 1−  6 ×(−  1 )＝1＋  2 ＝  7  5  3  5  5 　(3)　7a＋b−5a＋10b＝2a＋11b 　(4)　3√3−2√3＋√3＝2√3 　(5)　(4x2＋4xy＋y2)−(x2＋4xy＋4y2) 　　　　＝3x2−3y2 ２ 両辺×6より， 　2(x−4)＋3(7−x)＝5×6 　2x−8＋21−3x＝30 　−x＝17より，x＝−17 ３ ∠xの外角＝360−(80＋105＋70＋45)＝60° 　　よって，∠x＝180−60＝120° ４(1)145〜150cmの相対度数＝2÷40＝0.05 　［　　］＝1−(0.05＋0.1＋0.3＋0.2＋0.1) 　　　＝1−0.75＝0.25 　(2) 40×(0.3＋0.2＋0.1)＝40×0.6＝24人 ５ 偶数（確率1/3）1回だから， 　1枚目が偶数になる確率＝  1 ×(  2 )2＝  4  3  3 27 　2，3枚目が偶数になる確率も同様だから， 　求める確率＝  4 ×3＝  4 27  9
27大阪府	【A選択】 １　(1)　−5　　(2)　5×4÷6＝ 20 ＝ 10   6  3 　(3) 6x＋4　(4) 16x2y2÷(−2y)＝−8x2y 　(5) 5√2−3√2＝2√2 ２　3x2−7xy−6y2 ３   3√5 . ＝ 3√5 √5√5 5 ４　(x＋8)(x−3)＝0より，x＝−8，3 ５　10より大きいのは，次の3通り 　　　(A，B)＝(5，6)　(6，5)　(6，6) 　　よって，   3 ＝  1 36 12 ６　ア　y＝2(x＋10)＝2x＋20（１次関数） 　　イ　y＝x2　（２乗に比例） 　　ウ  　1 xy＝20より，y＝ 40 （反比例）   　2  x 　　エ　y＝3x（比例）　　　よって，エ ７　(1)　 y＝  1 ×32＝  9  2  2 　 (2)　B (−1，  1 ) だから，  2 　　y＝2(x＋1)＋  1 より，y＝2x＋  5  2  2	31鳥取県	１ (1)　3−7＋2＝−2 　(2)   　8×3 ＝ 24 ＝  4  　9×2 18  3 　(3)　3√2−√2＝2√2 　(4)　3x−6−x＋1＝2x−5 　(5)   6ab×4ab2 ＝3b3  8a2 ２ ２乗して比較すると， 　ア   　4 ＝ 12 　イ   　2 　ウ   　2 ＝  6  　3  9  　9  　3  9 　エ   　4 　　よって，ア   　9 ３　(x＋8)(x−8) ４　−3y＝−12x＋11より， 　　y＝4x− 11 　または，y＝ 12x−11  3 3 ５　解の公式より， 　x＝−3±√9＋8＝−3±√17 ６　ＡＣは直径だから，∠ＡＥＣ＝90°より， 　　　　∠x＝90−36＝54° ７　正面から見た立面図は二等辺三角形で， 　　ま上から見た平面図は正方形 　　　　よって，エ 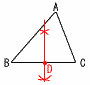８　（答は右図） 　線分ＢＣの垂直二等分線を引き 　　　中点をＤとする。 ９　△AEDと△ABCにおいて， 　　AE:AB＝5:10＝1:2　･･･ア 　　AD:AC＝6:12＝1:2　･･･イ 　アイより，AE:AB＝AD:AC＝1:2　･･･ウ 　　∠EAD＝∠BAC（共通）　･･･エ 　ウエより， 　2組の辺の比と間の角が等しいから， 　　△AED∽△ABC
	【B選択】 １　9×(−2)−6×(−4)＝−18＋24＝6 ２ 　　　　　　　(√2＋1) 　  　 　(√2−1)(√6＋√3)  − 4＋2√3 √3　1 4 　　＝2−1− 2＋√3 ＝− √3 2 2 ３　2x2−3x−5−x2＋2x−1＝0 　　　x2−x−6＝0で，(x−3)(x＋2)＝0 　　　よって，x＝3，−2 ４　中央の数をxとすると， (x−2)＋(x−1)＋x＋(x＋1)＋(x＋2)＝2015 　5x＝2015より，x＝403 　よって，403＋2＝405 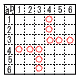５　（右図参照） 　条件にあうのは○で，10通り 　　よって，   10 ＝  5  36 18  ６　平均値＝97÷25≒3.9，中央値＝4 　a＝13，b＝12，c＝10，d＝12だから，ウ ７　Ａ(0,−1)，Ｂ(−3,−  9 )だから，   4 　ＡＢ2＝(0＋3)2＋(−1＋  9 )2＝9＋  25 ＝ 169  4  16  16 　　Ｃ(0，k)とすると，ＣＡ2＝(k＋1)2 　　(k＋1)2＝ 169 より，k＋1＝ 13  16  4  　よって，k＝ 13 −1＝  9  4  4
28兵庫県	１　4　　　２  10−21 ＝−  11  7×5  35 ３　√2＋ 　4√2. ＝√2＋2√2＝3√2. √2√2 ４　(x＋3)(x−6)＝0より，x＝−3，6 ５　y＝  a に(4，−4)を代入して，  x 　　−4＝ a で，a＝−16 4 　y＝− 16 にx＝2を代入して，y＝− 16 ＝−8   x  2 ６　ＯＡ＝ＯＣ（半径）と∠ＢＡＣ＝90°より， 　　∠x＝∠ＯＡＣ＝90−40＝50° ７　△ＡＤＥ∽△ＡＢＣ（相似比2:3）より， 　　　12:△ＡＢＣ＝22:32＝4:9 　よって，△ＡＢＣ＝12×9÷4＝27cm2 　〜　２番問題（おまけ）　〜 １　最多は（y＝）13人で，４点 ２　x＋y＝35−(2＋9＋6)＝18　･･･ア 　　2＋2x＋27＋4y＋30＝3.4×35 　　2x＋4y＝119−59で，x＋2y＝30･･･イ 　イ−アより，y＝12で，アに代入して，x＝6 　　　　よって，x＝6，y＝12 ３　35人の中央値は，高い方からも18番目で， 　　これが3点（9人）になればよいから， 　6＋y＋9＝18より，y＝3 　6＋y＋1＝18より，y＝11 　　よって，ア　3人以上　　イ　11人以下	32島根県	１　10＋(−3)＝10−3＝7 ２　(√7)2−(√3)2＝7−3＝4 ３　2）60 　　2）30 　　3）15 　　　　5　　　　よって，22×3×5 ４   9a2×2 ＝6a  3a ５　解の公式より， 　　x＝  3±√9＋8 ＝  3±√17  2×1  2 ６　y＝  a より，a＝xy＝(−5)×6＝−30   x ７　目の出方は全部で，6×6＝36通り 　　このうち，積が4となるのは， 　　(大，小)＝(1,4)　(2,2)　(4,1) の3通り 　よって，求める確率＝  3 ＝  1 36 12 ８　ウとエ 　ウ　ＡＤ//ＢＣより，∠Ａ＋∠Ｂ＝180° 　　∠Ａ＝∠Ｃより，∠Ｃ＋∠Ｂ＝180° 　　　　よって，ＡＢ//ＤＣ 　　　2組の対辺が平行となる 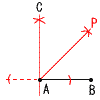　エ　∠Ａ＝∠Ｃ，∠Ｂ＝∠Ｄで， 　　　2組の対角が等しい ９　50×0.18＝9人 10　（右図） �@ ＢＡを延長し，垂線ＡＣを引く �A ∠ＢＡＣの二等分線ＡＰを引く