| 【 B 選 択 】 |
| 1 |
(−3)2×(−2)−6×(−22)
|
5 |
 アルファベットの書いてある6枚のカードA,B,C,D,E,Fが,右のように,左から右へとアルファベット順に横1列に並んでいる。 アルファベットの書いてある6枚のカードA,B,C,D,E,Fが,右のように,左から右へとアルファベット順に横1列に並んでいる。
大小二つのさいころを同時に投げ,大きいさいころの出る目の数をa,小さいさいころの出る目の数をbとする。aとbが異なる場合は,左からa番目のカードと左からb番目のカードとを交換し,aとbが等しい場合は,カードを交換しないことにする。大小二つのさいころを同時に投げるとき,カードCがカードDより右側になる確率はいくらですか。1から6までのどの目が出ることも同様に確からしいものとして答えなさい。
|
| 2 |
| (√2−1)(√3+√6) |
− |
(√3+1)2 |
| √3 |
4 |
|
| 3 |
二次方程式 (2x−5)(x+1)−(x−1)2=0 を解きなさい。
|
6 |
借りた本の
冊数(冊) |
生徒の
人数(人) |
| 7 |
5 |
| 6 |
3 |
| 5 |
2 |
| 4 |
3 |
| 3 |
4 |
| 2 |
2 |
| 1 |
6 |
| 合計 |
25 |
生徒25人がある期間に図書室から本を借りた。右の表は,本を借りた生徒の人数を冊数別にまとめたものである。借りた本の冊数の平均値,中央値をもとに,a,b,c,dを次のように定める。
a
|
借りた本の冊数が平均値より大きい生徒の人数 |
b
|
借りた本の冊数が平均値より小さい生徒の人数 |
c
|
借りた本の冊数が中央値より大きい生徒の人数 |
d
|
借りた本の冊数が中央値より小さい生徒の人数 |
次のア〜エの式のうち,正しいものを一つ選び,記号を○で囲みなさい。
ア a=b イ a=c ウ b=d エ c=d |
| 4 |
連続する五つの自然数の和が2015になるとき,この五つの自然数のうち最大の自然数を求めなさい。
|
7 |
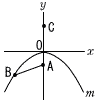 表す。Aはy軸上の点であり,Aのy座標は−1である。Bはm上の点であり,Bのx座標は−3である。AとBを結ぶ。Cはy軸上の点であり,Cのy座標はAのy座標より大きく,CA=BAである。このとき,Cのy座標を求めなさい。求め方も書くこと。ただし,x軸の1目もりの長さとy軸の1目もりの長さは等しいものとする。 表す。Aはy軸上の点であり,Aのy座標は−1である。Bはm上の点であり,Bのx座標は−3である。AとBを結ぶ。Cはy軸上の点であり,Cのy座標はAのy座標より大きく,CA=BAである。このとき,Cのy座標を求めなさい。求め方も書くこと。ただし,x軸の1目もりの長さとy軸の1目もりの長さは等しいものとする。
|
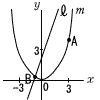 A,Bはm上の点であり,そのx座標はそれぞれ3,−1である。l は,点Bを通り傾きが2の直線である。
A,Bはm上の点であり,そのx座標はそれぞれ3,−1である。l は,点Bを通り傾きが2の直線である。 表す。Aはy軸上の点であり,Aのy座標は−1である。Bはm上の点であり,Bのx座標は−3である。AとBを結ぶ。Cはy軸上の点であり,Cのy座標はAのy座標より大きく,CA=BAである。このとき,Cのy座標を求めなさい。求め方も書くこと。ただし,x軸の1目もりの長さとy軸の1目もりの長さは等しいものとする。
表す。Aはy軸上の点であり,Aのy座標は−1である。Bはm上の点であり,Bのx座標は−3である。AとBを結ぶ。Cはy軸上の点であり,Cのy座標はAのy座標より大きく,CA=BAである。このとき,Cのy座標を求めなさい。求め方も書くこと。ただし,x軸の1目もりの長さとy軸の1目もりの長さは等しいものとする。