|
(25)滋賀県 | 学習日 月 日( ) |
|
(25)滋賀県 | 学習日 月 日( ) |
〜 印刷して、紙の上でやってネ! (文字サイズを小にするとA4に収まります)〜
| 1 | (1) . (2) . (3) 12xy2÷(−2y)2 . (4) (x+2)(x−5)−6x .
. |
5 | 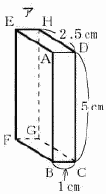 図1のような直方体アを, 図2のように,水平な面Rの上に,面BCGFを下にして置く。 このとき,辺BCを通る直線を 図1のような直方体アを, 図2のように,水平な面Rの上に,面BCGFを下にして置く。 このとき,辺BCを通る直線を次に,アをイに向けて倒すと,アに続いてイ,ウの順に倒れる。 次の(1),(2)の問いに答えなさい。 ただし,直方体が倒れても,辺CG,JL,OQの面R上の位置は変わらないものとする。 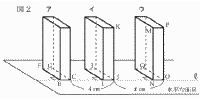 (1) 図3のように,直方体イの頂点Kがウの辺MNの中点 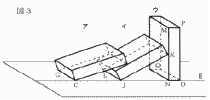 にあたった。 図4は,倒れだす前のウのようすを面MNOPを正面とする方向から見た図である。 点Jを,コンパスと定規を使って作図しなさい。 ただし,作図に使った線は消さないこと。 にあたった。 図4は,倒れだす前のウのようすを面MNOPを正面とする方向から見た図である。 点Jを,コンパスと定規を使って作図しなさい。 ただし,作図に使った線は消さないこと。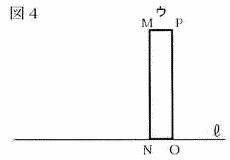 (2) 図5のように,直方体ウが倒れ,直方体アとイの重なる 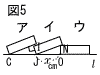 部分が,ぴったりとつくときのxの値を求めなさい。 部分が,ぴったりとつくときのxの値を求めなさい。. |
||||
| 2 | 次の2次方程式を解きなさい。 (x−3)2=x . |
||||||
| 3 | 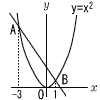 図のように,関数 y=x2 のグラフ上に,2点A,Bがある。 A,Bのx座標がそれぞれ−3,1であるとき,2点A,Bを通る直線の式を求めなさい。 図のように,関数 y=x2 のグラフ上に,2点A,Bがある。 A,Bのx座標がそれぞれ−3,1であるとき,2点A,Bを通る直線の式を求めなさい。. |
||||||
| 4 | 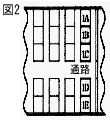 な座席の特急列車で,太郎さん,花子さん,次郎さん,明さん,広美さんの5人がくじを1枚ずつ引いてそれぞれの座席に座る。 5人のうちの太郎さんと花子さんが,隣りどうしになる確率を求めなさい。 ただし,通路を隔てた場合は,隣りどうしとしないこととする。 また,どのくじの引き方も同様に確からしいとする。 な座席の特急列車で,太郎さん,花子さん,次郎さん,明さん,広美さんの5人がくじを1枚ずつ引いてそれぞれの座席に座る。 5人のうちの太郎さんと花子さんが,隣りどうしになる確率を求めなさい。 ただし,通路を隔てた場合は,隣りどうしとしないこととする。 また,どのくじの引き方も同様に確からしいとする。. |
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] [答のペ−ジに進む] |