|
���@���@�S | ||||
| 25�@���ꌧ�@�`�@32�@������ | |||||
|
���@���@�S | ||||
| 25�@���ꌧ�@�`�@32�@������ | |||||
�` ������āA���̏�ł���ăl�I �i�����T�C�Y�����ɂ���Ƃ`�S�Ɏ��܂�܂��j�`
| 25���ꌧ | �P�@(1)�@2�|3���|1 �@�@(2)�@4a�|9�{7a��11a�|9 �@�@(3)�@12xy2��4y2��3x �@�@(4)�@x2�|3x�|10�|6x��x2�|9x�|10
�Q�@��������ƁCx2�|7x�{9��0 �@���̌������C
�R�@�`(�|3�C9)�C�a(1�C1)������C
�@�@����āC�@y���|2x�{3 �S�@������͑S���ŁC5�~4�~3�~2�~1��120�ʂ� �@�@���̂����C�ׂ�ǂ����̍�����́C�`�Ƃa�C�a�Ƃb�C �@�@�@�@�@�c�Ƃd�̂R�ʂ�ŁC�t���l���ĂU�ʂ�B �@�@���̂Ƃ��C���̂R�l�̍�����́C3�~2�~1��6�ʂ�
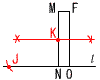 �T �@(1)�@�E�} �@�@�@�EMN�̒��_K���Ƃ�B �@�@�@�EKJ��MN�ƂȂ�_��l��ɂƂ�B �@(2)�@��CIJ�ŁCCI��4�CIJ��1���C �@�@�@�@�@x����42�|12����15 �@ |
29�ޗnj� |
�@�@(4)�@x2�|2xy�|3y2��x2�|11xy�|3y2�@�@ �Q�@�㎮�~3�|�������C11y��11�ŁCy��1 �@�@������㎮�ɑ�����āCx�{2��4�ŁCx��2 �@�@�@����āCx��2�Cy��1 �R�@(x�|2)(x�|6)��0���Cx��2�C6 �S�@3��5����45�ŁC��36����45����49 �@�@�@�@�܂�C6��3��5��7�ƂȂ邩��C�@�b �T�@y��ax�ɁC(2�C�|6)��������ƁC�|6��2a �@�@�@�@a���|3�ƂȂ邩��C����y���|3x �@�@�@�@�����x���|1�������āC�@y��3 �U�@0���b�̊K���ŁC
 �V�@�i�E�}�Q�Ɓj �V�@�i�E�}�Q�Ɓj�@a��8�`11�ɂȂ�悢�B a��8�̂Ƃ��C2+6�C3+5�C4+4�C �@�@�@5+3�C6+2��5�ʂ� a��9�̂Ƃ��C3+6�C4+5�C5+4�C �@�@�@6+3��4�ʂ� a��10�̂Ƃ��C4+6�C5+5�C6+4��3�ʂ� a��11�̂Ƃ��C5+6�C6+5��2�ʂ�
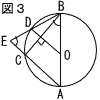
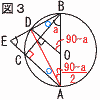 �W �i�E�}�Q�Ɓj �W �i�E�}�Q�Ɓj�@AB�͔��a������C�ڂb��90�� �@�@����āC�ڂa�`�b��90�|������A �@�ڂa�`�c��(90�|a)/2�@����C �@�A�|�C���C �@�@�@�ڂb�a�c���ڂb�`�c��(90�|��)/2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26���s�{ | �y�O���z
�S�@�^����(2x�|y)2��(2�~19�|45)2 �@�@�@�@�@��(38�|45)2��(�|7)2��49 �T�@6�~(�|3/2)���|9 �U�@x��3�������āC27�|3��3a�{12 �@�@�@3a��12���Ca��4 �V�@x2�{8x�|9��0 �@�@(x�{9)(x�|1)��0���C�@x���|9�C1
�@�@(�)�@���ϒl��(1�~3�{2�~2�{3�~5�{4�~6 �@�@�@�@�@�@�@�{5�~3)��20��61��20��3.05 �@�@(�)�@�ŕp�l��6�l�ŁC4�� �@�@(�)�@�����l��10�l�ڂ�11�l�ڂŁC3�� �@�@�@�@�@�@�@����āC�G �y�����z
�@�@�@�@�@��8�|6��2 �S�@y��a/x �ɁC(6�C�|4)�������āC �@�@�@�@�|4��a/6�ŁCa���|24 �@�@y���|24/x �ɁCx���|3�������āC �@�@�@�@y��(�|24)/(�|3)��8 �T�@�㎮�~2�{�������C11x��33�ŁCx��3 �@�@������㎮�ɑ�����āCx��3�Cy���|5 �U�@(x�{3)(x�{12)��0���Cx���|3�C�|12  �V�@�i�E�}�Q�Ɓj �V�@�i�E�}�Q�Ɓj�@�@���`�}����C�@3/8 �W�@�A�@20�~0.35��7 �@�@�C�@20�|7�|10��3 �@�@�E�@3��200.15�@�@�@ |
30�a�̎R�� | �P�@(1) 2
�@�@(3)�@8x�|8y�{6x�|12y��14x�|20y
�@�@(5)�@x2�{2x�|x2�|x�{12��2x�{12 �Q�@�T�@�@�i -2�C-1�C0�C1�C2 �j �R�@���a3cm�̔���������C
�@�\�ʐρ�4�~32��2�{32��18�{9�� �@�@�@�@�@�@��27��cm2 �S
�@�@�A�|�C���C2x�|2y��10�ŁCx�|y��5����G �@�@�E�C�G���Cx2�|y2��(x�{y)(x�|y)��3�~5��15 �T�@(1)�@�A�@2�@�@�C�@3�@�@�E�@6 �@�@(2)�@3��15��0.2 �@ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27���{ | �y�O���z
�R�@�Q������x��2��������ƁC �@�@�@4a�{8�|6a�|14��0���Ca���|3 �@�@�|3x2�{4x�{18�|14��0 �@�@�@�@3x2�|4x�|4��0 �@�@�@(3x�{2)(x�|2)��0���Cx���|2/3 �S�@by���|ax�{c
�@����Đ������̂́C�C �y����z �P�@(1)�@�P�{8��9�@�@(2)�@6a�{4b�|3a�{b��3a�{5b
�Q�@���ӂ�4�{���āC �@�@�@3x�{9���|4x�|40 �@�@�@�@�@7x���|49���Cx���|7 �R�@(3x)2�|82��(3x�{8)(3x�|8) �S�@5a�{2b��500 �T�@�A�C�E |
31���挧 |
�@�@(4)�@5a�|3b�|2b�{4a��9a�|5b
�S�@���ӂ�3�{���āC���E����ꂩ����ƁC
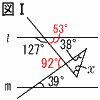 �U�@�i�E�}�Q�Ɓj �U�@�i�E�}�Q�Ɓj�@��x��180�|38�|(53�{39) �@�@�@�@��142�|92��50���@�@�@ �V�@���a3cm�̋�������C
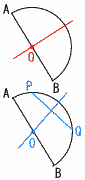 �@���aAB�̐��������i�ԁj�� �@���aAB�̐��������i�ԁj���@�@�@AB�̌�_��O�Ƃ���B �@�i�ʉ��j �@�K���Ȍ�PQ�̐��������i�j �@�@�@��AB�̌�_��O�Ƃ���B �X (1)�@���o�`�r�Ɓ��o�b�c�ŁC �@�ڂo�`�a���ڂo�b�c�i�ʂa�c�̉~���p�j �@�ڂo�a�`���ڂo�c�b�i�ʂ`�b�̉~���p�j �@�@�@�Q�g�̊p������������C �@�@�@�@�@�@�@���o�`�r�䁢�o�b�c (2)�@7�FPD��4�F6���C �@�@�@�@�@PD��42/4��21/2cm |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28���Ɍ� | �P�@20
�R�@2��3�{4��3��6��3 �S�@���̌������C
�@�@�_(3�C2)��ʂ邩��Cy��2(x�|3)�{2 �@�@�@�@y��2x�|4
�V�@20�l�̒����l�́C10�l�ڂ�11�l�ڂŁC �@�@�@���ɂS��������C�S�� �@�@�@�@�@�ŕp�l�͓x�����傫��(4�l)�̂R���@�@�@ |
32������ | �P�@9�|2��7 �Q�@5��2�|2��2�{3�~3��2��12��2
�T�@(x�|2)(x�|3)��0���C�@x��2�C3 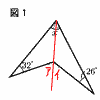 �U�@�i�E�}�Q�Ɓj �U�@�i�E�}�Q�Ɓj�@��x��(��|32)�{(��|26) �@�@�@��(��{�)�|58��130�|58 �@�@�@��72�� �V�@��52�{62�{82 �@�@����25�{36�{64��5��5cm �W�@32�~10��90��cm3 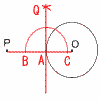 �X�@�A�@8�~35��280�i�������j �X�@�A�@8�~35��280�i�������j�@�@�E�@2�{20��22�i�������j �@�@�@���������āC�@�A�C�E 10�@�i�E�}�j �@�EPO�Ɖ~�̌�_A���Ƃ� �@�EAB��AC�ƂȂ�Q�_B�CC���Ƃ� �@�EBQ��CQ�ƂȂ�_Q���Ƃ� �@�EAQ���ڐ��@ |
| �m�g�b�v�ɖ߂��n �m�O�y�[�W�ɖ߂��n�@�m���y�|�W�ɐi���n |