全国公立高校入試 　１番問題　【平成２５年春】

（２）　青森県

学習日　　　 　　 月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

［　前　期　］		［　後　期　］
１	ア　−3−4 　　　　　　　　　　　　　　　　　　　　　　　　　 .	１	ア　5−7 　　　　　　　　　　　　　　　　　　　　　　　　　 .
	イ　− 2 ÷ 4 3 9 　　　　　　　　　　　　　　　　　　　　　　　　 .		イ　6÷(− 2 ) 3 　　　　　　　　　　　　　　　　　　　　　　　　　 .
	ウ　(−2)3＋5×(−7) 　　　　　　　　　　　　　　　　　　　　　　　　　 .		ウ　−3×(−4)−22 　　　　　　　　　　　　　　　　　　　　　　　　　 .
	エ　7ｘ−12＋4(7−ｘ) 　　　　　　　　　　　　　　　　　　　　　　　　　 .		エ　5(ａ−2ｂ)＋2(ａ＋ｂ) 　　　　　　　　　　　　　　　　　　　　　　　　　 .
	オ　√24＋  30 −√6 √6 　　　　　　　　　　　　　　　　　　　　　　　　　 .		オ　√18＋ 　4 . √2 　　　　　　　　　　　　　　　　　　　　　　　　　 .
２	ａ＝3，ｂ＝−2のとき，次の式の値を求めなさい。 　　　4ａ2÷6ａｂ×3ｂ2 　　　　　　　　　　　　　　　　　　　　　　　　　 .	２	次の等式をｂについて解きなさい。 　　　2ａ＋3ｂ＝5 　　　　　　　　　　　　　　　　　　　　　　　　　 .
３	次の連立方程式を解きなさい。 　　　｛ ｘ＋2ｙ＝4   ｙ＝3ｘ−5    　　　　　　　　　　　　　　　　　　　　　　　　　 .	３	次の式を因数分解しなさい。 　　　ｘ ｙ2−4ｘ 　　　　　　　　　　　　　　　　　　　　　　　　　 .
４	次の式を因数分解しなさい。 　　　ｘ2−18ｘ＋72 　　　　　　　　　　　　　　　　　　　　　　　　　 .	４	次の二次方程式を解きなさい。 　　　　ｘ2−3ｘ＋1＝0 　　　　　　　　　　　　　　　　　　　　　　　　　 .
５	関数　ｙ＝2ｘ2　について，ｘの変域が−2≦ｘ≦3のとき，ｙの変域を求めなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 .	５	ｘ 　□  −2 　0 　ｙ 　4  　3 　0 　右の表で，ｙがｘに比例するとき，□にあてはまる数を求めなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 .
６	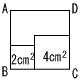右の図のように，正方形ＡＢＣＤの内部に２つの正方形があり，それぞれの面積は 2cm2，4cm2 である。正方形ＡＢＣＤの面積を求めなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 . 　　　＜以下７〜８は略＞	６	生徒 Ａ Ｂ Ｃ Ｄ Ｅ Ｆ Ｇ  Ｈ Ｉ 時間 6.2 　5 8.5 　7 6.5 　9 4.8 5.8 4.5 　右の表は，９人の生徒Ａ〜Ｉ のある１日の睡眠時間をまとめたものである。この９人の睡眠時間の中央値を求めなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 . 　　　＜以下７〜８は略＞

［トップに戻る］ ［前ページに戻る］　［次ペ−ジに進む］ ［答のペ−ジに進む］　やさしい　ややむずかしい