|
(31) 鳥取県 | 学習日 月 日( ) |
|
(31) 鳥取県 | 学習日 月 日( ) |
| 1 | . |
6 |
点Aのx 座標をaとして,次の(1),(2)に答えなさい。 (1) aの値を求めなさい。 . (2) x の変域が-2≦ x ≦aのとき,この関数のyの変域を求めなさい。 . (7番 代表値の問題は省略) |
||||
. |
|||||||
| (3) √6(√3-1) . |
|||||||
| (4) 10ab2÷2b×5a . |
8 | 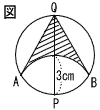 このとき,線分QA,線分QB,点Oを含む弧ABで囲まれた斜線部分の図形の面積を求めなさい。 . |
|||||
| 2 | 2a+3b=5 を b について解きなさい。 . |
||||||
| 3 | t2+5t-6 を因数分解しなさい。 . |
9 | 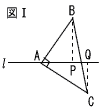 右の図Ⅰのように,AB=ACである直角二等辺三角形ABCと頂点Aを通る直線 右の図Ⅰのように,AB=ACである直角二等辺三角形ABCと頂点Aを通る直線このとき,次の(1),(2)に答えなさい。 (1) 直線 なお,作図に用いた線は。消さずに残しておきなさい。  (2) △ABPと△CAQに着目して,AP=CQとなることを証明しなさい。 |
||||
| 4 | 二次方程式 x2+3x-5=0 を解きなさい。 . |
||||||
| 5 | 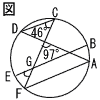 右の図において,6点A,B,C,D,E,Fは円周上の点であり,点Gは弦BEと弦CFとの交点である。AF//BEのとき,∠EGFの大きさを求めなさい。 右の図において,6点A,B,C,D,E,Fは円周上の点であり,点Gは弦BEと弦CFとの交点である。AF//BEのとき,∠EGFの大きさを求めなさい。. |
| [トップに戻る] [前ページに戻る] [次ペ-ジに進む] [答のペ-ジに進む] |