全国公立高校入試 　１番問題　【平成２４年春】	正　答　４
	25滋賀県　〜　32島根県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

25滋賀県	１　(1)　3−5＝−2 　　(2)　8ａ−6−6ａ＝2ａ−6 　 (3) . 8ｘ2ｙ×2ｙ ＝ｙ2 　16ｘ2　 　　(4)　ｘ2＋8ｘ＋16−ｘ−7＝ｘ2＋7ｘ＋9 　 (5) . 2√3 − 　2√3. ＝ √3−2√3 ＝− √3 　6　 √3√3 　　　3　　　 　3 ２　ｘ2＋5ｘ−14＝0 　　(ｘ＋7)(ｘ−2)＝0より，ｘ＝−7，2 ３　ｙ＝ａｘ2に，(2，−8)を代入して， 　　　　−8＝4ａより，ａ＝−2 　　ｙ＝−2ｘ2にｘ＝5を代入して， 　　　　ｙ＝−2×52＝−50 ４　 (1)　長さが１となるのは，隣り合う点を結ぶときで， 　　　　ＡＢ，ＢＣ，･･･，ＦＡの６通り 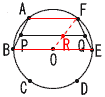　　6点から2点を結ぶ方法は， 　　　　6×6÷2＝18通り 　　よって，6÷18＝1/3 (2)　（右図参照） 　　ＡＦ＝ＰＲ＝ＢＯ＝1 　　ＲＱ＝1/2ＯＥ＝1/2 　　　　よって，ＰＱ＝1＋1/2＝3/2 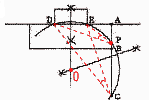５　（右図参照） 　∠ＤＣＥ＝∠ＤＰＥより， 　円周角が等しくなればよい。 　４点Ｄ，Ｅ，Ｐ，Ｃを通る円の 　　　中心Ｏを求めるため， 　線分ＤＥとＥＣの 　　　垂直二等分線を引き， 　　　その交点をＯとする。 　円Ｏと線分ＡＣの交点にＰをとるとよい。	29奈良県	［特　色］ １　(1)　−4　　　(2)　10ｘ−9ｙ　　　(3)　2ｂ 　　(4)　ｘ2＋2ｘ＋1−8＝ｘ2＋2ｘ−7 　　(5)　3√3＋√3＝4√3 ２　3ｘ−ｘ＝9＋5 　　　　2ｘ＝14より，ｘ＝7 ３　(ｘ−6)(ｘ＋2)＝0より，ｘ＝6，−2 ４　３平方の定理より， 　　　　ＡＢ＝√(72−42)×2＝√(49−16)×2 　　　　　　＝2√33cm ５　５人から２人選ぶ方法は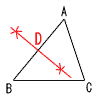， 　　　 . 5×4 ＝10通り 2×1 　　このうち，Ａが選ばれるのは４通り 　　よって求める確率は， 4 ＝ 2 10 5 ６　（右図参照） (1)　辺ＡＢの垂直二等分線を 　　引き，交点をＤとする。 (2)　△ＡＤＥ∽△ＡＢＣより， 　　　　△ＡＤＥ：△ＡＢＣ＝1：4 　　　△ＡＤＥ：24＝1：4より， 　　　　△ＡＤＥ＝6cm2 ７　(1)　速さと時間は反比例だから，ウ 　　(2)　比例定数 ａ＝60×20＝1200より， 　　　　　　ｙ＝ 1200 　ｘ　 ［一　般］ １　(1)　−42　　(2)　5ｘ−4ｘ＋8ｙ＝ｘ＋8ｙ 　 (3) . ａ×6ａｂ ＝3ｂ 　2ａ2　 　　(4)　ｘ2−6ｘｙ＋9ｙ2＋8ｘｙ＝ｘ2＋2ｘｙ＋9ｙ2 ２　−7/3＝−2.333･･･，√11＝3.***より， 　　　　整数は，−2，−1，･･･，3の　６個 ３　上式＋下式×3より， 　　　　7ｘ＝28で，ｘ＝4 　　これを上式に代入して， 　　　　4＋3ｙ＝1より，ｙ＝−1 　　よって，ｘ＝4，ｙ＝−1 ４　ｘ2−5ｘ−6＝0 　　(ｘ−6)(ｘ＋1)＝0より，ｘ＝6，−1 ５　体積＝ 1 ×52×9＝75cm3 3 ６　白の碁石がｘ個とすると， 　 . 10 ＝ 　100 . より， 80 ｘ＋100 　　10(ｘ＋100)＝80×100を解いて， 　　10ｘ＝8000−1000で，ｘ＝700 　　　　およそ700個で，ア
26京都府	１　25−36÷2＝25−18＝7 ２ . 4(2ｘ＋1)−3(ｘ−3) ＝ 8ｘ＋4−3ｘ＋9 　　　　　3×4　　　 　　　　12　　　 　　＝ 5ｘ＋13 　　12　 ３　√3＋4√3− 　6√3 . ＝5√3−2√3 √3√3 　　＝3√3 ４　ｙ (ｘ2＋4ｘ−21)＝ｙ (ｘ＋7)(ｘ−3) ５　上式＋下式×2より，7ｘ＝35で，ｘ＝5 　　これを上式に代入して，5−4ｙ＝17 　　　　よって，ｘ＝5，ｙ＝−3 ６　解の公式より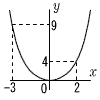， 　　　ｘ＝ −7±√72−4×1×5 　　　　2×1　　　 　　　　＝ −7±√49−20 ＝ −7±√29 　　　　　2　　　　　 　　　2　　　 ７　ｘ＝−3のとき，ｙ＝(−3)2＝9 　　ｘ＝2のとき，ｙ＝22＝4 　　ところが，ｘ＝0のとき，ｙ＝0 　　　　よって，0≦ｙ≦9	30和歌山県	１　(1)　−3 　 (2) . 　 3×4×1 . ＝− 12 ＝− 2 2×(−3)×7 42 7 　　(3)　3ｘ＋4ｙ−2ｘ＋3ｙ＝ｘ＋7ｙ 　 (4)　2√5＋ 　5√5 . 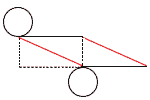＝2√5＋√5＝3√5 √5√5 　　(5)　ａ2−9ｂ2−ａ2＋3ａｂ＝3ａｂ−9ｂ2 ２　解の公式より， 　　　ｘ＝ −(−3)±√(−3)2−4×1×2 　　　　　　　　2×1　　　　　　　 　　　　＝ 3±√9−4 ＝ 3±√5 　　　2　　　 　　2　 ３　生徒の総数は， 　　1＋3＋6＋9＋11 　　　　　＋4＋1＝35人 　よって，中央値は18番目　　　　　　　　　　　　３冊 ４　（右図参照） 　　　　　平行四辺形 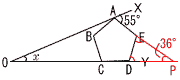５　（右図参照） 　正五角形の外角は， 　　360÷5＝72° 　よって， 　∠Ｐ＝180−72×2 　　　 ＝36° 　したがって，∠ｘ＝55−36＝19°
27大阪府	［前期］ １　−2＋5＝3 ２　3ａ−4ｂ＋2ａ＋6ｂ＝5ａ＋2ｂ ３　4√3−3√3＝√3 ４　. 1×9 − 3 ＝ 3−6 ＝− 3 6×4 4 　8　 8 ５　. 18ｘ2ｙ3 ＝2ｘ2ｙ 　9ｙ2　 　〜２番問題（おまけ）〜 １　(ｘ−7)(ｘ＋6)＝0より，ｘ＝7，−6 ［後期　Ａ］ １　ア　−5＋3＝−2 　　イ　2ａ−6ｂ＋ａ＋8ｂ＝3ａ＋2ｂ 　　ウ　4ａ2ｂ2÷2ａ＝2ａｂ2 　　エ　8√5−4√5＝4√5 ２　両辺×3より， 　　　　4ｘ＋3＝−6ｘ＋18 　　　　 　10ｘ＝15で，ｘ＝15/10＝3/2 ３　(ｘ−6)(ｘ＋5) ４　積が6以下となるのは，表より14通り。 　 １ ２ ３ ４ ５ ６ １ 1 2 3 4 5 6 ２ 2 4 6 　 　 　 ３ 3 6 　 　 　 　 ４ 4 　 　 　 　 　 ５ 5 　 　 　 　 　 ６ 6 　 　 　 　 　 よって求める確率は， 14 ＝ ７ 36 18 ［後期　Ｂ］ １　5−24＋60＝41 ２　9ｘ2−9ｘｙ−4ｙ2−ｘ2＋4ｙ2＝8ｘ2−9ｘｙ ３ . 4(4√3−2√2) − 3（3√3−3√2) 　　　　12　　　　 　　　　12　　　 　　＝ 16√3−8√2−9√3＋9√2 　　　　　　　　　12　　　　　　　 　　＝ 7√3＋√2 　　　12　　 ４　ｙ＝ ｃ−ａｘ ＝− ａ ｘ＋ ｃ より，エ 　　ｂ　 ｂ ｂ ５　ａ＋ｂがａｂの約数になるのは，下の表より 　　　　５通りだから，求める確率は，5/36 　ａ　. ２ ３ ６ ４ ６ 　ｂ　. ２ ６ ３ ４ ６ ａ＋ｂ ４ ９ ９ ８ 12 　ａｂ ４ 18 18 16 36	31鳥取県	１　　(1)　−2＋3＝1 　　 (2) . 2−9 − 7 　6　 6 　　　(3)　√18−√6＝3√2−√6 　　 (4) . 10ａｂ2×5ｂ ＝25ａ2ｂ 　　　2ｂ　　 ２　3ｂ＝5−2ａより， 　　 ｂ＝ 5−2ａ 　または，ｂ＝ −2ａ＋5 　　3　 　　3　　 ３　(ｔ＋6)(ｔ−1) ４　解の公式より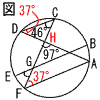， 　　　ｘ＝ −3±√32−4×1×(−5) 　　　　　　2×1　　　　　 　　　　＝ −3±√9＋20 ＝ −3±√29 　　　　　2　　　　 　　　2　　　 ５　（右図参照） 　△ＣＤＨで， 　　∠Ｄ＝180−46−97＝37° 　∠Ｆ＝∠Ｄ＝37°(円周角) 　∠Ｇ＝∠Ｆ＝37°(錯角) ６　 (1)　△ＯＡＢ＝1/2×8×ａ＝12 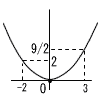　　　　　4ａ＝12より，ａ＝3 (2)　（右図参照） 　ｘ＝−2のとき，ｙ＝1/2×22＝2 　ｘ＝3のとき，ｙ＝1/2×32＝9/2 　　　よって，0≦ｙ≦9/2 ７　（省略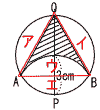） ８　（右図参照） 　円Ｏ−正三角形ＡＢＱ 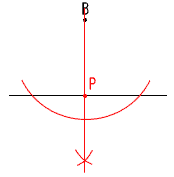　　＝32π− √3 ×(3√3)2 　4 　　＝9π− 27√3 　　4　 　ア＝イ＝ウ＝エ＝ 1 (9π− 27√3 ) 3 　　4　 　　＝3π− 9√3 　4　 円Ｏ−ア×4＝32π−(3π− 9√3 )×4 　4　 　　＝9π−12π＋9√3＝9√3−3π(cm2) ９　（右図参照） (1)　Ｂからに垂線をおろし， 　　　　　交点Ｐをとる (2)　△ＡＢＰと△ＣＡＱで， 　　　　∠Ｐ＝∠Ｑ＝90° 　　　　ＡＢ＝ＣＡ（等辺） 　　　　∠Ｂ＝∠Ａ＝90−∠ＢＡＰ 　　直角三角形で， 　　　　斜辺と１鋭角が等しいから， 　　△ＡＢＰ≡△ＣＡＱ 　　　　よって，ＡＰ＝ＣＱ
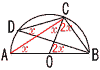28兵庫県	１　2＋6＝8 ２ . 20−27 ＝− ７ 　　30　 30 ３　5√3−4√3＝√3 ４　解の公式より， 　　ｘ＝ −3±√32−4×1×(−5) 　　　　　　2×1　　　　　　 　　　＝ −3±√9＋20 ＝ −3±√29 　　　　　2　　　　 　　　2　　　 ５　（右図参照）　ＡとＣを結ぶ 　∠ＢＤＣ＝ｘ とすると， 　　　∠ＯＡＣ＝∠ＯＣＡ＝ｘ 　　　∠ＢＯＣ＝∠ＢＣＯ＝2ｘ 　ＡＢは直径で，∠ＡＣＢ＝90° 　　　ｘ＋2ｘ＝3ｘ＝90°より，ｘ＝30° ６　中央値は，20と21番目の平均値で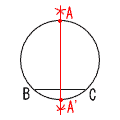， 　　　　どちらも同じで，２点 　　最頻値は，人数が14人の３点 ７　（右図参照） 　弦ＢＣの垂直二等分線と， 　　円周との交点をとればよい。 　　　（右図のＡまたは，Ａ'になる）	32島根県	１　−4＋6＝2 ２　4√2＋3√2−6√2＝√2 ３　. 18ｘ2ｙ×10 ＝4ｘ ｙ 　　5×9ｘ　 ４　(ｘ−3)(ｘ＋2) ５　解の公式より， 　ｘ＝ −5±√52−4×3×(−1) ＝ −5±√37 　　　　　　2×3　　　　　 　　　6　　 ６　４人なら，1000÷4＝250羽 　　20人なら，1000÷20＝50羽 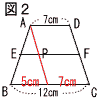　よって，50÷250＝ １ 倍 ５ ７　2ｘ＋1＜10 ８　総得点は， 　　　1×1＋2×1＋3×2 　　　　　　＋4×4＋5×2＝35点 　　総人数は， 　　　　　1＋1＋2＋4＋2＝10人 　よって平均点は， 　　　　　35÷10＝3.5点 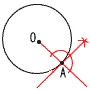９　（右上図参照） 　　ＡからＤＣに平行線を引き， 　　　ＥＦとの交点をＰとすると， 　　ＥＰ＝5÷2＝2.5，ＰＦ＝7 　　よって，ＥＦ＝2.5＋7＝9.5cm 10　（右上図参照） 　　ＯＡを延長し，Ａから垂線を引けばよい。