全国公立高校入試 　１番問題　【平成２３年春】

（４２）　長崎県

学習日　 　　 月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

Ａ		Ｂ
１	6＋(−8)×2 　　　　　　　　　　　　　　　　　　　　　　　　　 .	１	(1＋√2)2− 　4　. √2 　　　　　　　　　　　　　　　　　　　　　　　　　 .
２	. 3 ＋ 1 5 10 　　　　　　　　　　　　　　　　　　　　　　　　　 .	２	ａ3ｂ×(−3ａ)3÷ａ2ｂ 　　　　　　　　　　　　　　　　　　　　　　　　 .
３	√27−√12 　　　　　　　　　　　　　　　　　　　　　　　　　 .	３	連立方程式　｛　. ｘ＋ｙ − ｘ ＝1 　2　 3 ｘ＋2ｙ ＝ 2 　　　　　　　　　　　　　　　　　　　　　　　　　 .
４	6ｘ2ｙ× ｙ2 2 　　　　　　　　　　　　　　　　　　　　　　　　　 .
５	ｘ＝3，ｙ＝−1のとき，2ｘ2＋ｙ3　の値を求めよ。 　　　　　　　　　　　　　　　　　　　　　　　　　 .	４	２次方程式　(ｘ＋1)(ｘ−1)＝5ｘ−ｘ2　を解け。 　　　　　　　　　　　　　　　　　　　　　　　　　 .
６	連立方程式　｛　 ｘ＋2ｙ＝4 　を解け。 2ｘ＋ｙ＝−1 　　　　　　　　　　　　　　　　　　　　　　　　　 .	５	相似な２つの四角形Ｐ，Ｑがあって，ＰとＱの相似比は2：3である。Ｐの面積が8cm2のとき，Ｑの面積は何cm2か。 　　　　　　　　　　　　　　　　　　　　　　　　　 .
７	２次方程式　ｘ2＋3ｘ＋1＝0　を解け。 　　　　　　　　　　　　　　　　　　　　　　　　　 .	６	関数　ｙ＝ａｘ2　について，ｘの値が1から3まで増加するときの変化の割合が12である。　このとき，ａの値を求めよ。 　　　　　　　　　　　　　　　　　　　　　　　　　 .
８	ｙはｘに比例し，ｘ＝2のとき，ｙ＝6である。　このとき，ｙをｘの式で表せ。 　　　　　　　　　　　　　　　　　　　　　　　　　 .
９	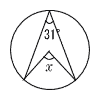右の図のような円Ｏにおいて，∠ｘの大きさを求めよ。 　　　　　　　　　　　　　　　　　　 .	７	√( 540 )　の値が整数になるような 　ｎ 自然数のうち，最も小さいものを求めよ。 　　　　　　　　　　　　　　　　　　　　　　 .
10	相似な２つの四角形Ｐ，Ｑがあって，ＰとＱの相似比は1：2である。Ｐの面積が5cm2のとき，Ｑの面積は何cm2か。 　　　　　　　　　　　　　　　　　　　　　　　　　 .	８	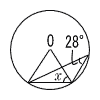右の図のような円Ｏにおいて，∠ｘの大きさを求めよ。

［トップに戻る］ ［前ページに戻る］　［次ペ−ジに進む］ ［答のペ−ジに進む］　やさしい　ややむずかしい