全国公立高校入試
　１番問題　【平成２３年春】
　（３１）　鳥取県 　学習日　 　　 月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１ (1)　 8−(−2)

　　　　　　　　　　　　　　　　　　　　　　　　　 .		 ７ 　袋の中に白玉だけがたくさん入っている。白玉の個数を推測するために、同じ大きさの赤玉50個を白玉の入っている袋の中に入れ、その中から40個の玉を無作為に抽出し、白玉と赤玉の個数を調べた後に袋の中にもどす実験を数回おこなったところ、平均して赤玉は5個入っていた。この結果をもとに、もともと袋の中に入っていた白玉の個数は、およそ何個と推測されるか求めなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　 .　　
(2)　　. 1 − 2
2 3
　　　　　　　　　　　　　　　　　　　　　　　　　 .
(3)　(√5−√3)2

　　　　　　　　　　　　　　　　　　　　　　　　　 .		 ８ 　右の図のように、Ｏを中心としＡＢを直径とする半径4ｃｍの半円の周上に、弧ＡＢを３等分する点をとり、点Ａに近い方から順にＣ、Ｄとする。
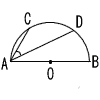(1)　∠ＣＡＤの大きさを求めなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　 .

(2)　線分ＡＣ、線分ＡＤ、弧ＣＤで囲まれた図形の周の長さを求めなさい。
　　　　　　　　　　　　　　　　　　　　　　　　　 .
(4)　4ａ2ｂ÷2ａｂ

　　　　　　　　　　　　　　　　　　　　　　　　　 .
２ 　ａ2−ａ−12　を因数分解しなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　 .
３ 　二次方程式　2ｘ2＋3ｘ−4＝0　を解きなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　 .		 ９ 　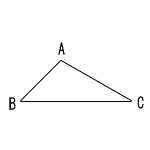右の図の△ＡＢＣにおいて、∠ＢＡＣの二等分線と、辺ＡＣの垂直二等分線との交点Ｐを、コンパスと定規を用いて作図しなさい。
　なお、作図に用いた線は、消さずに残しておきなさい。
　
４ 　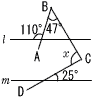右の図のように、線分ＡＢ、ＢＣ、ＣＤが、直線、ｍと交わっている。//ｍのとき、∠ｘの大きさを求めなさい。


　　　　　　　　　　　　　　　　　　　 .
５
一次関数　ｙ＝ 1 ｘ＋1 (−2≦ｘ≦1)　･･･ア
2
のｙの変域と、関数　ｙ＝ａｘ2 (−2≦ｘ≦1) のｙの変域は同じであった。
(1)　アのｙの変域を求めなさい。
　　　　　　　　　　　　　　　　　　　　　　　　　 .

(2)　ａの値を求めなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　 .　		 10 　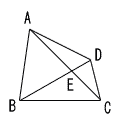右の図の対角線の交点をＥとする四角形ＡＢＣＤにおいて、∠ＢＣＡ＝∠ＤＣＡ、ＢＡ＝ＢＥならば、△ＡＢＣ∽△ＥＤＣである。
　このことを証明しなさい。
［証明］
６ 　右の図のように黒い石を使って図形を規則的に作るとき、15番目の図形を作るために必要な黒い石は何個か求めなさい。

　　　　　　　　　　　　　　　　 .

［トップに戻る］ ［前ページに戻る］　［次ペ−ジに進む］ ［答のペ−ジに進む］　やさしい　ややむずかしい