|
正 答 4 | ||||
| 25 滋賀県 〜 32 島根県 | |||||
|
正 答 4 | ||||
| 25 滋賀県 〜 32 島根県 | |||||
| 25滋賀県 | 1 (1)−12+7=−5
(4) x2+8x+15−x2−9x=−x+15
2 解の公式より
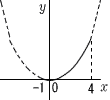 3 (右図参照) x=−1のとき, y=1/2×(−1)2=1/2 x=4のとき, y=1/2×42=8 x=0のとき,y=0 よって,0≦y≦8 |
29奈良県 | [特色選抜] 1 (1) −18 (2) x−2y (3) 2a (4) x2−4−3=x2−7 (5) 2√2+3√2=5√2 2 7x=14より,x=2 3 (x−4)(x+3)=0より,x=4,−3 4 各辺を2乗すると,2.25<a<9だから, 整数a=3,4,5,6,7,8 よって,6個 5 底面の半径6cm,高さ7cmの円すいだから, 1/3×62π×7=84πcm3 6 x+43=107より, x=107−43=64° 7 (1/2)3=1/8 [一般] 1 (1) −4 (2) 6x+2y−x+5y=5x+7y (3) 6ab×(−a3)=−6a4b (4) x2−4xy+4y2+5xy =x2+xy+4y2 2 √10≒3.16,22/7=3.14だから, 最大数は,√10 3 上式+下式×3より, 5x=10で,x=2 これを上式に代入して, 4+3y=1で,y=−1 よって,x=2,y=−1 4 解の公式より,
底面積=1/2×4×3=6 側面積=(4+3+5)×7=84 よって,6×2+84=96cm2 |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 26京都府 | 1 9+2×(−16)=9−32=−23
−6=2aで,a=−3 5 (x−8)(x+2) 6 解の公式より,
底面の円周=6π おうぎ形の弧=16π×(x/360)=2/45πx よって,2/45πx=6π x=135° |
30和歌山県 | 1 (1) −2
(3) 2x−6y−x+2y=x−4y (4) 3√2+√2−2√2=2√2 (5) a2+4ab+4b2−a2+4ab−4b2=8ab 2 (x−5)(x+2) 3 横の長さ=(100−2x)÷2=50−x 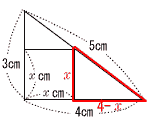 4 (右図参照) x:3=(4−x)=4より, 4x=12−3x 7x=12
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| 27大阪府 | [前期] 1 −6−4=−10
3 4a+b−6a+2b=−2a+3b
5 7−4=3 〜2番問題(おまけ)〜 1 (x+9)(x−3) [後期] 1 (1) −2+5=3 (2) 3a−2b−a+3b=2a+b
(4) 2√6−3√6=−√6 2 3(3x+2)=5(2x−1) 9x+6=10x−5 −x=−11で,x=11 3 (x−3)(x−7) 4 2枚の取り出し方は全部で,5×4÷2=10通り 和が3の倍数となるのは, 1と2,1と5,2と4の3通り よって求める確率は,3/10 5 a=−1とすると, ア −a=1 イ −1/2a=1/2 ウ 1/a=−1 エ a=−1 オ 2a=−2 よって最大値は,ア |
31鳥取県 | 1 (1) 8+2=10
(4) 2a 2 (a−4)(a+3) 3 解の公式より,
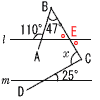 4 (右図参照) 4 (右図参照)∠E=110−47=63° ∠x=∠E+25=88° 5 (1) x=−2のとき, y=1/2×(−2)+1=0 x=1のとき, y=1/2×1+1=3/2 よって,0≦y≦3/2 ・・・イ (2) y=ax2 (−2≦x≦1)では, x=−2のとき,y=4a よって,0≦y≦4a ・・・ウ イとウが同じだから, 4a=3/2で,a=3/8 6 左下から斜めに足して考えると, 1+2+3+ ・・・ +14+15 =(1+15)+(2+14)+・・・+(7+9)+8 =16×7+8=112+8=120 [別解] (15×15−15)÷2+15=120 7 白玉をx個とすると,
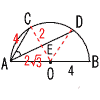 およそ350個 およそ350個8 (1) ∠CAD=∠COD÷2 =60÷2=30° (2) △ACEで, AC=4,AE=2√3 AD=2√3×2=4√3 弧CD=8π×1/6=4/3π よって,4+4√3+4/3πcm 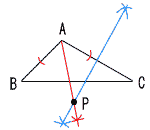 9 (右図参照) 9 (右図参照)ア ∠BACの二等分線 (赤線) イ 辺ACの垂直二等分線 (青線) ウ 2本の交点をPとする 10 [証明] △ABCと△EDCで, ∠BCA=∠DCE(仮定) ∠BAC=∠DEC=∠AEB(底角) よって,2組の角が等しいから, △ABC∽△EDC |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 28兵庫県 | 1 −3+8=5
3 3√5−2√5=√5 4 (x+5)(x−2)=0 x=−5,2 5 ∠x (弧ABの円周角)=弧BCの円周角×2 =28×2=56°
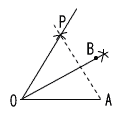 7 (右図参照) 7 (右図参照)ア OAを1辺とする正三角形 OAPをかく イ ∠AOPの二等分線OB をひく |
32島根県 | 1 5+3=8 2 3√2−6√2−5√2=−8√2
5x−10=2x−4 3x=6で,x=2 5 解の公式より,
7 DE:2=3:8より,DE=3/4cm 8 ∠ACB=∠D=180−90−35=55° 9 32π×4=36πcm3 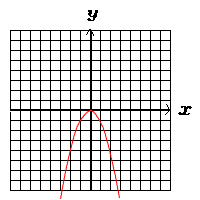 10 (右図参照) 10 (右図参照) |
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] |