全国公立高校入試 　１番問題　【平成２２年春】

（３）　秋田県

学習日　 　　 　　月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （問題数が多いので，Ａ４で２枚）〜

次の１〜15の中から，指示された８問について答えなさい。
１	−3，−1，0，2，4の５つの数から異なる２つの数を選んで積を求める。 (1)　積が最も大きくなる２つの数を書きなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 . (2)　積が最も小さくなる２つの数を書きなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 .	９	学さんは自宅から1200m離れた駅に向かった。　はじめは毎分80mの速さで歩き，途中から毎分160mの速さで走ったところ，12分かかって駅に着いた。　このとき，学さんが歩いていた時間をｘ分とすると， 　80ｘ＋160(12−ｘ)＝1200 という方程式ができる。　 　この方程式において，160(12−ｘ)はどのような数量を表しているか，書きなさい。 　 　　　　　　　　　　　　　　　　　　　　　　　　　.
２	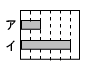図のように，等間隔の目盛りがついた紙の上に，２本のテープが平行に置かれている。 (1)　アのテープの長さを6cmとするとき，イのテープの長さを求めなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 . (1)　アのテープの長さをａcmとするとき，イのテープの長さを，ａを用いた式で表しなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 . .	10	一の位が０でない２けたの自然数Aがあり，この数の十の位の数字と，一の位の数字を入れかえた数をBとする。 　√(A＋B) と √(A−B) がともに自然数になるとき，Aの値を求めなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 .
３	(−4ａ)2× １ ｂ÷2ａｂ ４ 　　　　　　　　　　　　　　　　　　　　　　　　　 .	11	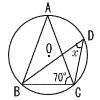右の図において，点Oを中心とする円の周上に，４点A，B，C，Dがある。　AB=AC，∠ACB=70°のとき，∠ｘの大きさを求めなさい。 　　　　　　　　　　　　　　　　　　　　　.
４	√45−√10×√2 　　　　　　　　　　　　　　　　　　　　　　　　　.	12	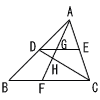右の図のように，三角形ABCがある。　点D，Eはそれぞれ辺AB，ACの中点である。　点Fは辺BC上の点であり，線分AFと線分DE，DCとの交点をそれぞれG，Hとする。　DH：HC＝１：３，GE=3cmのとき，線分BFの長さを求めなさい。 　　　　　　　　　　　　　　　　　　　　　　.
５	等式　ｍ＝ 2ａ＋ｂ 　を，ｂについて解きなさい。 　　3　 　　　　　　　　　　　　　　　　　　　　　　　　　 .	13	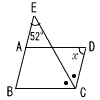右の図において，四角形ABCDは平行四辺形である。線分BAを延長した直線と∠BCDの二等分線の交点をEとする。　∠BEC=52°のとき，∠ｘの大きさを求めなさい。 　　　　　　　　　　　　　　　　　　　　　.
６	連立方程式　｛　 ｘ＋2ｙ＝4 　を解きなさい。 −3ｘ＋ｙ＝9 　　　　　　　　　　　　　　　　　　　　　　　　　 .	14	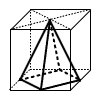右の図のように，立方体の１つの面の各辺の中点と，その面に平行な面の対角線の交点を頂点とする正四角すいがある。　立方体の１辺が6cmのとき，この正四角すいの体積を求めなさい。 　　　　　　　　　　　　　　　　　　　　　.
７	方程式　(ｘ＋4)(ｘ−4)＝3ｘ−6　を解きなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 .	15	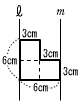右の図のように，１辺が3cmの正方形を３つ組み合わせた図形がある。　この図形を，直線を軸として１回転してできる立体をP，直線ｍを軸として１回転してできる立体をQとする。　PとQでは，表面積はどちらがどれだけ大きいか，求めなさい。 　　　　　　　　　　　　　　　　　　　　　 .
８	ある自然数ａを５で割ると，商がｂ，余りがｒ になった。　このとき，ｒ を ａ，ｂの式で表しなさい。 　　　　　　　　　　　　　　　　　　　　　　　　　 .