|
惓丂摎丂侾 | ||||
| 侾丂杒奀摴丂乣丂俉丂堬忛導 | |||||
|
惓丂摎丂侾 | ||||
| 侾丂杒奀摴丂乣丂俉丂堬忛導 | |||||
| 侾杒奀摴 | 侾丂(1)丂5亅9亖亅4 丂丂(2)丂7亄2亖11 丂丂(3)丂亅2亄4亖2 俀丂梌幃亖亅3倶倷2亖亅3亊(1/3)亊(亅1)2亖2 俁丂壓幃傛傝丆倶亖9亅3倷 丂丂偙傟傪忋幃偵戙擖偟偰丆3(9亅3倷)亄4倷亖17 丂丂丂丂倷亖2 丂丂偙傟傛傝丆倶亖3 丂丂傛偭偰丆倶亖3丆倷亖2 係丂倷亖倎/倶偵(3丆亅4)傪戙擖偟偰丆倎亖亅12 丂丂倷亖亅12/倶偵倷亖2傪戙擖偟偰丆倶亖亅6 俆丂偙偺棫懱偺懱愊偼丆 丂丂丂敿宎4cm丆崅偝10cm偺墌拰偲摍偟偄偐傜 丂丂42兾亊10亖160兾cm3丂丂丂 |
俆嶳宍導 | 侾丂(1)丂亅5亅3亅1亖亅9 丂丂(2)丂1/2亅7/8亖亅3/8 丂丂(3)丂6倶亄3倷亅5倶亄15倷亖倶亄18倷 丂丂(4)丂2亄2併2亄1亅4併2亖3亅2併2 俀丂倶2亅9亖亅2倶亅1 丂丂(倶亄4)(倶亅2)亖0傛傝丆倶亖亅4丆2 俁丂仮P仜仜偼慡晹偱15捠傝 丂丂偙偺偆偪丆捈妏嶰妏宍偼師偺3捠傝 丂丂丂丂仮PAD丆仮PBE丆仮PCF 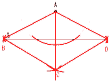 丂丂傛偭偰丆3/15亖1/5 丂丂傛偭偰丆3/15亖1/5係丂嘆A偐傜偵悅慄傪偍傠偟丆懳徧側揰C傪偲傞 丂丂嘇AC傪侾曈偲偡傞惓嶰妏宍傪偐偔 俆丂(A)丂岎揰P偺嵗昗偼楢棫曽掱幃傪夝偄偰丆
丂丂丂丂傛偭偰丆併倎亖3傛傝丆倎亖9 丂丂(俛)丂俠俧亄俢俫亄俥俧亄俤俫亄俫俧 丂丂丂丂丂丂丂亖4亄4亄2亄6亄3亖19cm丂丂 |
|||||||||||||||||||
| 俀惵怷導 | 乵慜婜乶 侾丂傾丂亅1丂丂僀丂亅4丂丂僂丂8亅5亖3 丂丂僄丂6倶亅5亅8倶亅2亖亅2倶亅7 丂丂僆丂5併3亅3併3亄2併3亖4併3 俀丂梌幃亖8倶倷2亖8亊3亊1亖24 俁丂(倶亅8)(倶亄3)亖0傛傝丆丂倶亖8丆亅3 係丂尦偺幃偵(1丆3)傪戙擖偡傞偲丆 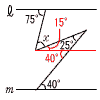
俆丂俙(亅2丆亅3)偲側傞偐傜丆 丂丂丂丂揰懳徧側揰偼丆(2丆3) 俇丂敿宎傪 倰 偲偡傞偲丆 丂丂丂丂2兾倰亖20兾亊(216/360) 丂丂丂丂2兾倰亖12兾傛傝丆丂倰亖6cm 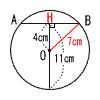 俈丂佢倶偺捀揰偐傜暯峴慄傪堷偔 俈丂佢倶偺捀揰偐傜暯峴慄傪堷偔丂丂丂丂佢倶亖75亅(40亅25)亖60亱 俉丂敿宎OH亖11亅4亖7cm 丂丂仮OBH偱丆嶰暯曽偺掕棟傛傝 丂丂丂丂BH2亖72亅42亖33 丂丂傛偭偰丆AB=BH亊2亖2併33cm 乵屻婜乶 侾丂傾丂亅6丂丂僀丂亅45丂丂僂丂11亅40亖亅29 丂丂僄丂8倶亄1丂丂僆丂倶2亄倶亅42 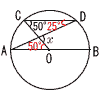 俀丂7倶亅3倶亖亅12亅8傛傝丆倶亖亅5 俀丂7倶亅3倶亖亅12亅8傛傝丆倶亖亅5俁丂5倶亅160亖9倷傛傝丆倶亖9/5倷亄32 係丂(倶亅7倷)2 俆丂倷亖倎倶2偵(2丆12)傪戙擖偟偰丆倎亖3 丂丂倷亖3倶2偵倶亖亅3傪戙擖偟偰丆倷亖27 俇丂倶亖亅6偺偲偒丆倷亖18/(亅6)亖亅3 丂丂倶亖亅2偺偲偒丆倷亖18/(亅2)亖亅9 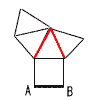 丂丂傛偭偰丆亅9亝倷亝亅3 丂丂傛偭偰丆亅9亝倷亝亅3俈丂佢AOC=佢OCD=50亱(嶖妏) 丂丂佢ADC=50亐2亖25亱(墌廃妏) 丂丂傛偭偰丆佢倶亖50亄25亖75亱 俉丂偹偠傟偺埵抲偵偁傞偺偼丆 丂丂AB偲暯峴偱側偔丆岎傢傜側偄曈 丂丂丂丂傛偭偰丆塃恾偺俀曈丂丂丂 |
俇媨忛導 | 侾丂亅3 俀丂5倶亅3倶亖2亄6傛傝丆倶亖4 俁丂梌幃亖4倎亄8亅倎亖3倎亄8亖3亊1/3亄8 丂丂丂丂亖1亄8亖9 係丂(倶亅2)(倶亅6) 俆丂俙俛偼捈宎偩偐傜丆佢俙俠俛亖90亱 丂丂丂傛偭偰丆佢俙俛俠亖180亅90亅50亖40亱 丂丂佢俙俷俠亖佢俛亊2亖40亊2亖80亱 丂丂丂傛偭偰丆屖俙俠亖3亊2亊兾亊(80/360) 丂丂丂丂丂丂丂丂丂丂丂丂亖6兾亊(2/9)亖4/3兾丂cm 乵俀斣栤戣乶丂乣偍傑偗乣 侾丂慖傃曽偼師偺俇捠傝偁傞丅 丂丂丂丂俙俛丆俙俠丆俙俢丆俛俠丆俛俢丆俠俢 丂丂偙偺偆偪丆抝彈偵側傞偺偼壓慄偺係捠傝 丂丂偟偨偑偭偰丆4/6亖2/3 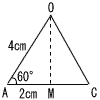 俀丂OM2亖42亅22亖12 丂丂丂傛偭偰丆俷俵亖併12亖2併3cm 丂丂懱愊亖1/3亊(4亊4亐2) 丂丂丂丂丂丂丂丂丂丂亊2併3 丂丂丂丂丂亖1/3亊8亊2併3 丂丂丂丂丂亖(16/3)併3丂cm3 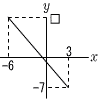 俁丂倶亖3偺偲偒丆倷亖亅7偵側傞偐傜丆 俁丂倶亖3偺偲偒丆倷亖亅7偵側傞偐傜丆丂丂丂倷亖倎倶偵戙擖偟偰丆 丂丂丂亅7亖3倎傛傝丆倎亖亅7/3 丂丂倷亖亅7/3倶偵丆倶亖亅6傪戙擖偟偰丆 丂丂丂倷亖亅(7/3)亊(亅6)亖14 丂丂丂傛偭偰丆14 丂 丂丂 |
|||||||||||||||||||
| 俁廐揷導 | 侾丂(1)丂2偲4丂丂(2)丂亅3偲4 俀丂(1)丂6丗倶亖2丗5傛傝丆倶亖15cm 丂丂(2)丂倎丗倷亖2丗5傛傝丆倷亖5/2倎 俁丂2倎 係丂3併5亅2併5亖併5 俆丂3倣亖2倎亄倐傛傝丆倐亖3倣亅2倎 俇丂倶亖亅2丆倷亖3 俈丂倶2亅16亖3倶亅6傛傝丆(倶亅5)(倶亄2)亖0 丂丂丂丂傛偭偰丆倶亖5丆亅2 俉丂倎亐5亖倐ゥ拋@傛傝丆倰亖倎亅5倐 俋丂(枅暘160m偺懍偝偱)憱偭偨嫍棧 10丂A亖10倶亄倷丆B亖10倷亄倶偲偡傞偲丆 丂丂丂丂A亄B亖11(倶亄倷)丆A亅B亖9(倶亅倷) 丂丂 傛偭偰丆倶亄倷亖11丆倶亅倷亖1傑偨偼4 丂丂丂丂楢棫偝偣偰寁嶼偡傞偲丆倶亖6丆倷亖5 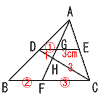 丂丂 偟偨偑偭偰丆A=65 丂丂 偟偨偑偭偰丆A=6511丂佢A亖180亅70亊2亖40亱 丂丂 傛偭偰丆佢倶亖佢A亖40亱 12丂仮HGD佷仮HFC傛傝丆 丂丂丂丂DG丗FC亖1丗3 丂丂 傑偨丆DG丗BF亖1丗2 丂丂 傛偭偰丆BF=3cm亊2亊(2/3)亖4cm 13丂佢DCE=52亱(嶖妏) 丂丂 傛偭偰丆佢倶亖180亅52亊2亖76亱 14丂1/3亊(3併2)2亊6亖36cm3 15丂P偺昞柺愊亖62兾亄6兾亊3亄12兾亊3亖126兾 丂丂 Q偺昞柺愊亖62兾亄12兾亊2亄6兾亊3亖162兾 丂丂 丂丂162兾亅126兾亖36兾 丂丂 傛偭偰丆Q偺曽偑36兾cm2戝偒偄丂 |
俈暉搰導 | 侾丂(1)丂4丂丂丂(2)丂亅7/6丂丂丂(3)丂亅併3
丂丂乣丂俀斣栤戣偺堦晹丂乮偍傑偗乯丂乣 侾丂忋幃亄壓幃亊3傛傝丆7倶亖21偱丆倶亖3 丂丂偙傟傪忋幃偵戙擖偟偰丆3亄3倷亖亅3 丂丂丂丂傛偭偰丆倶亖3丆倷亖亅2 俀丂梌幃亖倶2亅6倶亄9亄倶2亅2倶亅8 丂丂丂丂丂亖2倶2亅8倶亄1 俁丂倎亖倶倷亖亅2亊3亖亅6傛傝丆
係丂佢俙俷俛亖2佢俙俠俛亖2亊32亖64亱 丂丂佢倶亄32亖24亄64傛傝丆 丂丂丂丂佢倶亖24亄64亅32亖56亱 |
|||||||||||||||||||
| 係娾庤導 | 侾丂亅9 俀丂3/2 俁丂4亅2併7 係丂(倶亅3)(倶亅4)亖0傛傝丆倶亖3丆4 俆丂2倷亖9亅4倶
乵俀斣栤戣乶丂乣偍傑偗乣 侾丂仮俙俢俤佷仮俙俠俛傛傝丆俙俤丗俙俛亖俙俢丗俙俠 丂丂丂3丗俙俛亖2丗6傛傝丆俙俛亖9cm 俀丂佢倶 偺奜妏亖360亅(80亄75亄70亄60) 丂丂丂丂亖360亅285亖75 丂丂佢倶亖180亅75亖105亱 俁丂32兾亊5亖45兾cm3 |
俉堬忛導 | 侾丂亅4丂丂丂丂俀丂2亊9亅4亖14
俆丂2併2亅併10亅2併2亖亅併10 乵俀斣栤戣乶丂乣偍傑偗乣 侾丂(倶亄6)(倶亅6) 俀丂壓幃亊2亅忋幃傛傝丆倶亖亅3 丂丂偙傟傪壓幃偵戙擖偟偰丆亅9亄倷亖亅1傛傝丆倷亖8 丂丂丂丂傛偭偰丆倶亖亅3丆倷亖8 俁丂(倶亅6)(倶亄1)亖0傛傝丆倶亖6丆亅1 係丂倶亖2偺偲偒丆倷亖3亊22亖12 丂丂丂丂傛偭偰丆0亝倷亝12 俆丂梌幃亖倶(倶亄倷)亖(併5亄1)亊2併5 丂丂丂丂亖10亄2併5 |
| 乵僩僢僾偵栠傞乶 丂丂丂丂丂丂丂丂丂乵師儁亅僕偵恑傓乶 |
丂