全国公立高校入試
　１番問題　【平成２０年春】
　（１０）　群馬県 　学習日　 　　 月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１ 　3×(−4)

　　　　　　　　　　　　　　　　　　　　　　　　　 .
　		 ４ 　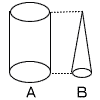右の図において，円柱Aと円すいBは高さが等しく，Aの底面の半径はBの底面の半径の２倍である。Aの体積はBの体積の何倍となるか，求めなさい。




　　　　　　　　　　　　　　　　　　　　　　　　　.
　　
２ 　−2ａ＋5ａ

. 　　　　　　　　　　　　　　　　　　　　　　　 .
３
　(8ａ−2ｂ)× 1
2
　　　　　　　　　　　　　　　　　　　　　　　　　 .
 ５ 　大小２つのさいころを同時に投げ，大きいさいころの出た目の数をａ，小さいさいころの出た目の数をｂとするとき，ｂ/ａが整数となる確率を求めなさい。


　　　　　　　　　　　　　　　　　　　　　　　　　.
　　
２　番　問　題　（おまけ）　
１ 　正の整数ａと負の整数ｂの差が３となるようなａとｂの組を，１組求めよ。

　　　　　　　　　　　　　　　　　　　　　　　　　 .
　		 ６ 　下の図の△ＡＢＣにおいて，辺ＢＣ上に点Ｐをとり，∠ＡＰＣ＝2∠ＡＢＣとなるような線分ＡＰを，コンパスと定規を用いて作図しなさい。
　ただし，図にかくのに用いた線は消さないこと。　　
２ 　1000円のａ％は何円か，式で表しなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　 .
　
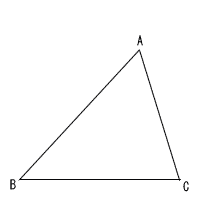３ 　１辺の長さがｘcmの正方形がある。この正方形の縦の辺を2cm，横の辺を3cmそれぞれ伸ばしてできた長方形の面積が，もとの正方形の面積の２倍となった。もとの正方形の１辺の長さを求めなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　 .
　

［トップに戻る］ ［前ページに戻る］　［次ペ−ジに進む］ ［答のペ−ジに進む］　やさしい　ややむずかしい