９栃木県	１　−6　　　２　5ａ3ｂ　　　３　(60ａ＋100ｂ)円 ４　与式＝(−3)2−7＝9−7＝2 ５　与式＝ｘ＋ｙ−2ｘ＋2ｙ＝−ｘ＋3ｙ ６　右図を参照して，面カ ７　4√2＋5√2＝9√2 ８　ｙ＝ａ/ｘにｘ＝5，ｙ＝−1を代入して， 　　　−1＝ａ/5で，ａ＝−5 　　よって，ｙ＝− ５ ｘ ９　∠ＡＤＢ＝∠ＡＣＢ＝31° 　　△ＡＢＤで，　よって， 　　　　∠ＢＡＤ＝180−80−31＝69°　 10　 2）　84　 　　　 　 2）　42　 　　　　 　 3）　21　 　よって，　　 　 　　　7 　　84＝22×3×7 11　ｘ：5＝3：8より，ｘ＝15/8 12　上式＋下式より，5ｘ＝20 　　　　よって，ｘ＝4，ｙ＝−6 13　1/3×22π×5＝20/3πcm3 14　ｘ＝1のとき，ｙ＝2×12＝2 　　 ｘ＝3のとき，ｙ＝2×32＝18 　　変化の割合＝ 18−2 ＝8 　3−1	13東京都	１　4＋4＝8 ２　5ａ−3ａ＋9ｂ−12ｂ＝2ａ−3ｂ ３　(√7)２−(√2)２＝7−2＝5 ４　−7ｘ＝7より，ｘ＝−1 ５　上式を下式に代入して， 　　　5ｘ−6(ｘ−3)＝9より，ｘ＝9 　　これを上式に代入して， 　　　ｙ＝9−3＝6 　　　よって，ｘ＝9，ｙ＝6 ６　ｘ(ｘ＋4)＝0より，ｘ＝0，−4 ７　求める取り出し方は， 　　(1,2) (1,4) (3,2) (3,4) (5,2) (5,4)の６通り 　　５枚から２枚取り出すのは，１０通り 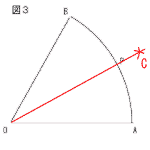　　よって，6/10＝3/5 ８　∠ＡＣＤ＝∠ＢＣＡ 　　＝180−54×2 　　＝180−108＝72° ９　２点Ａ，Ｂからコンパスを使って，　ＡＣ＝ＢＣとなる交点Ｃを作図する。 　　ＯＣと弧ＡＢの交点がＰとなる。
10群馬県	１　−12　　　２　3ａ　　　３　4ａ−ｂ ４　 ｘ 　または， 1 ｘ ２ 2 ５　ｘ2＋2ｘｙ＋ｙ2−2ｘｙ+2ｙ2＝ｘ2＋3ｙ2 　〜　２番問題（おまけ）　〜 １　ａ＝2，ｂ＝−1　または　ａ＝1，ｂ＝−2 ２　1000× 　ａ　 ＝10ａ　円 100 ３　１辺の長さをｘcmとすると， 　　(ｘ＋2)(ｘ＋3)＝2ｘ2 　　　ｘ2＋5ｘ＋6＝2ｘ2 　　　ｘ2−5ｘ−6＝0 　　　(ｘ−6)(ｘ＋1)＝0 　　ｘ＞0だから，ｘ＝6　cm ４　AとBの高さをｈ，Bの半径をｒとすると， 　　A=π(2ｒ)2ｈ，B=(1/3)πｒ2ｈ 　　よって，A÷B=4πｒ2ｈ÷(1/3)πｒ2ｈ 　　　　　　　　　　＝12　倍 ５　ｂ/ａ＝1/1，2/1，3/1，4/1，5/1，6/1， 　　　　　　2/2，4/2，6/2，3/3，6/3，4/4， 　　　　　　5/5，6/6　の14通り 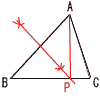　　よって，14/36＝7/18 ６　(1)　ＡＢの垂直二等分線を引く 　　(2)　ＢＣとの交点をＯとする 　　　（△ＰＡＢが二等辺三角形 　　　　となればよいから）	14神奈川県	１　8−13＝−5 ２　3＋7＝10 ３　 5−9 ＝− 4 　15　 15 ４　−3ａ ５　 7ｘ−4−4ｘ＋4 ＝ 3ｘ 　　　　8　　　 　8 ６　(6√2)/2＋2√2＝5√2 ７　ｘ２−6ｘ＋9−ｘ２−ｘ＋6＝−7ｘ＋15 　〜　２番問題の一部（おまけ）　〜 １　ｘ２−7ｘ−8＋5ｘ＝ｘ２−2ｘ−8 　　＝(ｘ−4)(ｘ＋2) ２　ｘ＋4＝±√6より，ｘ＝−4±√6 ３　ｘ＝−4のとき，ｙ＝16ａ 　　ｘ＝−2のとき，ｙ＝4ａ 　4ａ−16ａ　 ＝ −12ａ ＝−6ａ (−2)−(−4) 　　2　 　　よって，−6ａ＝2より，ａ＝−1/3 ４　与式＝ｘ２−ｙ２＝(3√2)２−(√5)２ 　　　＝18−5＝13
11埼玉県	１　−4−2＝−6 ２　5√3−3√3＝2√3 ３　与式＝(ｘ＋6)(ｘ−4)＝(14＋6)(14−4) 　　　＝20×10＝200 ４　ｘ−3＝±√5より，ｘ＝3±√5 ５　上式×2＋下式より， 　　　11ｘ＝22で，ｘ＝2 　　これを上式に代入して， 　　　6＋ｙ＝9で，ｙ＝3 　　よって，ｘ＝2，ｙ＝3 ６　ｙ＝ａｘ２に(1，−2)を代入すると， 　　−2＝ａ×12より，ａ＝−2 ７　ｘｙ＝16より，ｙ＝16/ｘ ８　∠ＡＯＢ＝20×2＝40° 　　∠ＣＯＥ＝(360−40)÷2＝160 　ｘ＝∠ＣＡＥ＝160÷2＝80° ９　1/3×△ABC×BF 　　　＝1/3×(1/2×6×6)×6 　　　＝1/6×63＝36cm3 10　ア　5×4÷2＝10試合 　　　イ　ｘ人のときの試合数は， 　　　　　 ｘ(ｘ−1) ＝55 　　2　　 　　これを解くと，ｘ２−ｘ−110＝0 　　　　(ｘ−11)(ｘ＋10)＝0より， 　　　　ｘ＞0だから，　ｘ＝11 　　　　　11人	15新潟県	１　 2＋1 ＝ 3 ＝ 1 　6　 6 2 ２　7+4＝11 ３　ｙ＝ ａ に，(2，4)を代入すると， ｘ 　　4＝ ａ より，ａ＝8 2 　　よって，ｙ＝ 8 ｘ ４　 6ｘｙ×(−3ｘ) ＝−2ｙ 　　　9ｘ2　　 ５　2ａ＝ｂ−5 　　　ａ＝ ｂ−5 　または，ａ＝ 1 (ｂ−5) 　2　 2 ６　上式×2＋下式より， 　　　7ｘ＝42で，ｘ＝6 　　これを上式に代入すると， 　　　12−ｙ＝15より，ｙ＝−3 　　よって，ｘ＝6，ｙ＝−3 ７　√48−√3＝4√3−√3＝3√3 ８　(ｘ＋8)(ｘ−5)＝0より，ｘ＝−8，5
12千葉県	１　−8　　　２　9＋3＝12 ３　 15ａ2ｂ×3ａｂ ＝−5ａ2 　　−9ａｂ2　 ４　両辺×3より，4ｘ−5＝3(2ｘ−9) 　　　4ｘ−6ｘ＝−27＋5で， 　　　−2ｘ＝−22より，ｘ＝11 ５　3√2−5√2＋ 　　8　　 √2√2 　　＝−2√2＋4√2＝2√2 ６　与式＝2(ｘ2＋5ｘ−6) 　　　　　＝2(ｘ＋6)(ｘ−1) 　〜　２番問題一部　（おまけ）　〜 １　与式＝ｘ2＋2ｘ−24＋25−ｘ2 　　　　　＝2ｘ＋1＝2×(1/2)＋1＝2 ２　ｘｙ＝12より，ｙ＝12/ｘで，　イ	16富山県	１　9−6＝2 ２　4ａ−9−ａ＋5＝3ａ−4 ３　500×(ａ/100)＝5ａ g ４　ｘｙ＝ａに，ｘ＝2，ｙ＝−6を代入すると， 　　　ａ＝2×(−6)＝−12 　　よって，ｙ＝− 12 ｘ ５　ＡとＢからＡＰ＝ＢＰとなる点Ｐをとり，ＯとＰを結ぶ ６　与式＝(ｘ＋ｙ)(ｘ−ｙ)＝(3−4)(3＋4)＝−7 ７　赤玉２個から２個取り出す方法は１通り 　　赤白玉４個から２個取り出す方法は 　　　　4×3÷2＝６通り 　よって，1/6 ８　 12×√6 ＝ 12√6 ＝2√6 √6×√6 　　6　 ９　与式＝ｘ2−14ｘ＋49 10　(ｘ＋12)(ｘ−2)＝0より，ｘ−−12，2