全国公立高校入試
　１番問題　【平成２０年春】
　（２）　青森県 　学習日　 　　 月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１ (1)　−6＋10

　　　　　　　　　　　　　　　　　　　　　　　　　 .

(2)　9÷(− ２ )
３

　　　　　　　　　　　　　　　　　　　　　　　　　 .

(3)　−42×3＋5


　　　　　　　　　　　　　　　　　　　　　　　　　 .

(4)　(ｘ−8)(ｘ＋7)

　　　　　　　　　　　　　　　　　　　　　　　　　 .

(5)　 　15 −√27＋√12
√3

　　　　　　　　　　　　　　　　　　　　　　　　　 .　　
　		 ４ 　絶対値が√７以下の整数をすべて書きなさい。


　　　　　　　　　　　　　　　　　　　　　　　　　.
　　
５ 　大小２つのサイコロを同時に投げるとき，出た目の数の積が３の倍数となる確率を求めなさい。



　　　　　　　　　　　　　　　　　　　　　　　　　.
　　　
６ 　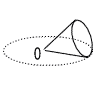底面の円の直径が４cm，母線の長さが12cmの円すいがある。右の図のように，この円すいを頂点Oを中心として平面上をすべることなくころがした。円すいが点線で示した円の上を１周してもとの位置にかえるまでに何回転するか求めなさい。



　　　　　　　　　　　　　　　　　　　　　　　　　.
　　
２ 　ｘ＝−2，ｙ＝5のとき，次の値を求めなさい。

　4ｘ2ｙ2÷8ｘｙ2×6ｘ


　　　　　　　　　　　　　　　　　　　　　　　　　.
　　		 ７ 　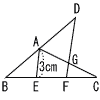右の図のように，△ABCの辺BAを延長し，BA=ADとなるように点Dをとり，辺BCを３等分する点をそれぞれE，F，とする。辺ACと線分DFの交点をGとする。
　このとき，DGの長さを求めなさい。

　　　　　　　　　　　　　　　　　　　　　.
　　
３ 　次の連立方程式を解きなさい。
　｛　 2ｘ＋3ｙ＝5
ｘ−2ｙ＝6


　　　　　　　　　　　　　　　　　　　　　　　　　.
 ８ 　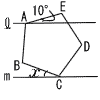右の図のように，正五角形ABCDEの頂点A，Cを通る直線をそれぞれ，ｍとする。
　//ｍであるとき，∠ｘの大きさを求めなさい。

　　　　　　　　　　　　　　　　　　　　　.
　　

［トップに戻る］ ［前ページに戻る］　［次ペ−ジに進む］ ［答のペ−ジに進む］　やさしい　ややむずかしい