１北海道	１　(1)　−7　 　　(2)　−24＋8＝−16 　　(3)　7＋5×3＝22 ２　12ｘ−10ｙ−9ｘ−21ｙ＝3ｘ−31ｙ ３　ある数をｘとすると， 　　　5ｘ−44＝−14 　　　　5ｘ＝30より，ｘ＝6 ４　ｙ＝ ａ に(2，8)を代入すると， ｘ 　　8＝ ａ より，ａ＝16 2 　　よって，ｙ＝ 16 ｘ ５　ｘ：30＝6：(6＋9) 　　　15ｘ＝180より，ｘ＝12 ６　１位は2しかないから， 　　　3×2×1×1＝6個 ７　平行でない，交わらない辺だから， 　　　ＣＧ，ＤＨ，ＥＨ，ＦＧ	５山形県	１　(1)　4−(−3)＝4＋3＝7 　　(2)　− 1 − 3×2 ＝− 1 − 2 2 5×3 2 5 　　　　＝ −5−4 ＝− 9 　　10　 10 　　(3)　4ｙ−1 　　(4)　6＋3√5−2√5−5＝1＋√5 ２　ｘ2＋2ｘ−3−5ｘ−7＝0 　　ｘ2−3ｘ−10＝0 　　　(ｘ−5)(ｘ＋2)＝0より，ｘ＝5，−2 ３　45以上の整数は，45，46，51〜56，61〜66 　　　で，2＋6＋6＝14個 　　２けたの整数は，6×6＝36個 　　よって，14÷36＝4/18 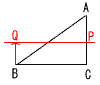４　(1)　ACの垂直二等分線をひき， 　　　　　　ACとの交点をPとする。 　　(2)　BからBQ=CPとなる 　　　　　　点Qをとる。 　　　　（または，PからPQ=CBとなる 　　　　　　点Qをとる） ５　 (A)　ウの１辺をｘcmとすると，イの面積は， 　　　(ｘ＋2)2＝50 　　　　ｘ＋2＝±√50＝±5√2 　　　　ｘ＞0だから，ｘ＝5√2−2　・・・(ｉ) 　　また，アウの面積の差は， 　　　(ｘ＋4)2−ｘ2＝8ｘ＋16　・・・(ii) 　　(i)を(ii)に代入して， 　　　8(5√2−2)＋16＝40√2cm2 (B)　∠CAD=90−50＝40°より， 　　　∠COD=40×2＝80° 　　　6π× 　80 ＝ 4 πcm 360 3
２青森県	１　(1)　10−6＝4 　　(2)　−9×3/2＝−27/2（または，13.5） 　　(3)　−16×3＋5＝−48＋5＝−43 　　(4)　ｘ2−ｘ−56 　　(5)　 15√3 −3√3＋2√3 　　3　 　　　　＝5√3−√3＝4√3　 ２　与式＝ 4ｘ2ｙ3×6ｘ ＝3ｘ2ｙ 　　8ｘｙ2　　 　　　　＝3×(−2)2×5＝60 ３　上式−下式×2より，7ｙ＝−7 　　　　よって，ｙ＝−1， 　　　これを上式に代入して， 　　　　2ｘ−3＝5で，ｘ＝4 　　　ｘ＝4，ｙ＝−1 ４　√4(2)＜√7＜√9(3)より， 　　　√7＝2.･･･ 　　したがって，±2，±1，0 ５　大小いずれかが3または6 　　　20÷36＝5/9 ６　円すい底面の円周は4π 　　点線の円周は半径12だから，24π 　　　よって，24π÷4π＝6回転 ７　ＡＥ//ＤＦより，ＤＦ＝3×2＝6 　　ＡＥ//ＧＨより，ＧＦ＝3÷2＝1.5 　　　よって，ＤＧ＝6−1.5＝4.5（9/2） ８　∠ｘ＝（108−10）−72＝26°	６宮城県	１　6−15＝−9 ２　8ａ−8−7ａ＋5＝ａ−3 ３　 √2×√5 ＝ √10 √5×√5 　5　 ４　ｘ2＋4ｘ−12＝0 　　(ｘ＋6)(ｘ−2)＝0 　　よって，ｘ＝−6，2 ５　ｘ＝−3のとき，ｙ＝(−3)2＝9 　　ｘ＝4のとき，ｙ＝42＝16 　　　よって，（ア　0　）≦ｙ≦（イ　16　） 　〜　２番問題　（おまけ）　〜 １　このクラスの生徒をｘ人とすると， 　　　3ｘ＋14＝4ｘ−9 　　　3ｘ−4ｘ＝−9−14より， 　　　　ｘ＝23人 ２　（青，白）＝(3，1)　(4，2)　(5，3)　(6，4) 　　　　の４通りだから，求める確率は 　　　 　4 ＝ 1 36 9 ３　1/3×52π×6＋1/3×52π×3 　　＝1/3×52π×9＝75πcm3
３秋田県	１　−2＋5＝3°C ２　(1)　1800÷20＝90円 　　(2)　20：ｘ＝ａ：□　より， 　　　□＝ ａｘ 20 ３　2ｘ＋2ｙ−5ｘ＋5ｙ＝−3ｘ＋7ｙ ４　 ａｂ2×4ａ2ｂ2 ＝−4ａｂ3 　　−ａ2ｂ　　 ５　4√2−5√2＝−√2 ６　与式＝(ｘ＋ｙ)(ｘ−ｙ) 　　　　＝(2008＋2007)(2008−2007) 　　　　＝4015×1＝4015 ７　両辺÷2より，(ｘ＋３）（ｘ＋5)＝24 　　　ｘ2＋8ｘ＋15＝24で，ｘ2+8ｘ−9＝0 　　　(ｘ＋9)(ｘ−1)＝0より，ｘ＝−9，1 ８　全長は2×8＝16ｍだから， 　　ｙ＝ １６ 　ｘ ９　子どもの人数をｘ人とすると， 　　 ｘ＋23 ＝ ｘ−2 　より， 　10　 　9　 　　9ｘ＋207＝10ｘ−20で， 　　　ｘ＝227本 10　3ｙ＝50−2ｘ＝2(25−ｘ)だから， 　　　　ｙは２の倍数となって，ｙ＝2，4，・・・ ｙ ２ ４ ６ ８ 10 12 14 16 ｘ 22 19 16 13 10 ７ ４ １ 　　表より，８個 11　∠Ｄ＝∠Ａ＝50°，∠ＢＣＤ＝90° 　　△ＢＣＤで，∠ｘ＝180−50−90＝40° 12　△ＡＤＥ∽△ＡＢＣより， 　　ＤＥ：15＝6：(6+4)で，10ＤＥ＝90 　　　よって，9cm １３　△OPSは直角二等辺三角形で， 　　　OP：4＝1：√2より， 　　　OP=４/√2＝2√2 　　　　よって，2√2×4√2＝16cm2 １４　1/3×ａ2×ａ＝(ａ3)/3 　　　(2ａ)3＝8ａ3 　　　よって，8ａ3÷(ａ3)/3＝24倍 １５　62π＋1/2×12π×8 　　　　＝36π＋48π＝84πcm2	７福島県	１　(1)　5 　　(2)　− 2×9 ＝− 3 3×8 4 　　(3)　4√3＋3√3＝7√3 　　(4)　3ａ＋6ｂ−4ａ＋4ｂ＝−ａ＋10ｂ ２　ｙ＝2ｘにｘ座標の値を代入すると， 　　ア　ｙ＝2×0＝0　（×） 　　イ　ｙ＝2×1＝2　（×） 　　ウ　ｙ＝2×2＝4　（○） 　　エ　ｙ＝2×4＝8　（×） 　　　よって，ウ 　〜　２番問題（おまけ）　〜 １　(80ａ＋120ｂ)円 ２　(ｘ−5)(ｘ＋4)＝0 　　　ｘ＝5，−4 ３　∠ｘ＝98−41＝57° ４　与式＝(ａ＋ｂ)(ａ−ｂ)となるから， 　　　(28＋22)(28−22)＝50×6＝300 ５　高さをｈとすると， 　　体積＝ 1 32πｈ＝18π 3 　　　3πｈ＝18πより，ｈ＝6cm
４岩手県	１　−4 ２　3ａ＋6−ａ＋1＝2ａ＋7 ３　3−2√3＋1＝4−2√3 ４　上式＋下式より，5ｘ＝10で，ｘ＝2 　　これを下式に代入して，4＋ｙ＝1 　　　よって，ｘ＝2，ｙ＝−3 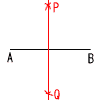５　ｘ(ｘ−5ｙ) 　〜　２番問題　（おまけ）　〜 １　(1)ＡとＢから， 　　　　ＰＡ＝ＰＢ，ＱＡ＝ＱＢと 　　　　なる点Ｐ，Ｑをコンパスでとる。 　　(2)ＰとＱを結ぶ 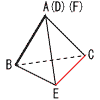２　平行でない，交わらない辺だから， 　　　　ＣＥ　　（右図参照） ３　4：ＣＤ＝2：3より，2ＣＤ＝12 　　　よって，ＣＤ＝6cm ４　AC2＝22＋12＝5より， 　　AC=√5cm	８茨城県	１　−8　　　２　4×5−6＝14 ３　 1 ＋ 7×2 ＝ 1 ＋ 1 4 6×7 4 3 　　　＝ 3＋4 ＝ 7 　12　 12 ４　−5ｘ＋10ｙ＋3ｘ−9ｙ＝−2ｘ＋ｙ ５　3√3−2√3＝√3 　〜　２番問題　（おまけ）　〜 １　3ｘｙ(ｘ＋2ｙ) ２　上式を下式に代入すると， 　　　2(3ｙ＋22)＋3ｙ＝8 　　　6ｙ＋3ｙ＝8−44 　　　　9ｙ＝−36より，ｙ＝−4 　　これを上式に代入して， 　　　　ｘ＝3×(−4)＋22＝10 　　よって，ｘ＝10，ｙ＝−4 ３　(ｘ−7)(ｘ-5)＝0より，ｘ＝7，5 ４　ｙ＝ａ/ｘにｘ＝3，ｙ＝2を代入すると， 　　2＝ａ/3より，ａ＝6 　　よって，ｙ＝ ６ ｘ ５　与式＝(ｘ−1)2＝(√3＋1−1)2 　　　＝(√3)2＝3