全国公立高校入試
　１番問題　【平成２０年春】
　（３）　秋田県 　学習日　 　　 月　　 　　日（　　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４で２枚に収まります）〜

次の１〜１５の中から，指示された８問について答えなさい。
１ 　土曜日の最低気温は−２°Cだったが，日曜日の最低気温は土曜日の最低気温より５°C高くなった。日曜日の最低気温を求めなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　 .
　		 10 　方程式　2ｘ＋3ｙ＝50　のグラフ上にあり，ｘ座標，ｙ座標がともに正の整数となる点は何個あるか，求めなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　.
　　
２ (1)　２０で1800円の灯油がある。この灯油 １の値段を求めなさい。

. 　　　　　　　　　　　　　　　　　　　　　　　 .

(2)　２０でａ円の灯油がある。この灯油 ｘの値段をａ，ｘを用いて表しなさい。

. 　　　　　　　　　　　　　　　　　　　　　　　 .
 11 　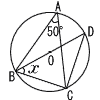右の図は，点Oを中心とする円であり，４点A，B，C，Dは円周上の点で，線分BDは円の直径である。∠BAC=50°のとき，∠ｘの大きさを求めなさい。




　　　　　　　　　　　　　　　　　　　　　　.
　　
３ 　2(ｘ＋ｙ)−5(ｘ−ｙ)　を計算しなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　 .
 12 　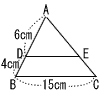右の図のように，三角形ABCがあり，点D，Eはそれぞれ辺AB，AC上の点で，DE//BCである。AD=6cm，DB=4cm，BC=15cmのとき，線分DEの長さを求めなさい。

　　　　　　　　　　　　　　　　　　　　　　.
　　
４ 　ａｂ2×(−2ａｂ)2÷(−ａ2ｂ)　を計算しなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　.
　　
５ 　4√2−√50　を計算しなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　 .
 13 　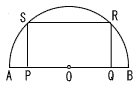右の図のように，線分ABを直径とする半円Oがある。２点P，Qは線分AB上の点，２点R，Sは弧AB上の点で，四角形PQRSはPQ=2QRの長方形である。半円Oの半径が4cmのとき，四角形PQRSの面積を求めなさい。
　　　　　　　　　　　　　　　　　　　　　　.
　　　
６ 　ｘ＝2008，ｙ＝2007のとき，ｘ2−ｙ2の値を求めなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　 .
　
７ 　方程式　2(ｘ＋3)(ｘ＋5)＝48　を解きなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　 .
　		 14 　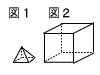図１は，底面の１辺の長さと高さが等しい正四角すいである。図２は，１辺の長さが図１の正四角すいの高さの２倍の立方体である。図２の立方体の体積は，図１の正四角すいの体積の何倍か，求めなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　.
　　
８ 　８等分すると１本の長さが２ｍになるテープを，ｘ等分すると１本の長さがｙｍになる。ｙをｘの式で表しなさい。

　　　　　　　　　　　　　　　　　　　　　　　　　 .
　
９ 　鉛筆を何人かの子どもたちに配る。１人に１０本ずつ配ると２３本足りなくなり，１人に９本ずつ配ると２本余る。鉛筆の本数は何本か，求めなさい。




　　　　　　　　　　　　　　　　　　　　　　　　　.
　　		 15 　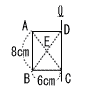右の図のように，直線と長方形ABCDがあり，辺CDは直線上にある。点Eは対角線AC，BDの交点で，AB=8cm，BC=6cmである。直線を回転の軸として三角形BCEを１回転させてできる立体の表面積を求めなさい。ただし，円周率はπとする。
　　　　　　　　　　　　　　　　　　　　　　.
　　

［トップに戻る］ ［前ページに戻る］　［次ペ−ジに進む］ ［答のペ−ジに進む］　やさしい　ややむずかしい