（４） 三平方定理の逆	学習日　 　 月　 　日（　　）
三角形の3辺で, 最長の辺の長さをcとするとき, (∠Cが最大角になって) 　c2＝a2＋b2ならば, 　直角三角形（∠C＝90°） 　c2＞a2＋b2ならば, 　鈍角三角形（∠C＞90°） 　c2＜a2＋b2ならば, 　鋭角三角形（∠C＜90°）

印刷して、紙の上でやってネ！　　印刷用

１	次の三角形の種類（直角,鈍角,鋭角）を答えなさい。（ ただし,図は正確とは限らない ）		２	3辺の長さが次のようになるとき,三角形の種類（直角,鈍角,鋭角）を答えなさい。
	(1)	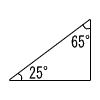三角形		(1)	8cm,6cm,10cm の三角形 ［解］ 最長の辺c＝　　だから, c2＝ a2＋b2＝ c2　　a2＋b2 となるから, 　　　　三角形
	(2)	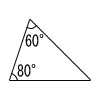三角形
	(3)	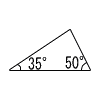三角形		(2)	4cm,2cm,3cm の三角形 ［解］ 最長の辺c＝　　だから, c2＝ a2＋b2＝ c2　　a2＋b2 となるから, 　　　　三角形
	(4)	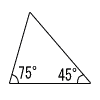三角形
	(5)	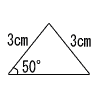三角形		(3)	4cm,4cm,3cm の三角形 ［解］ 最長の辺c＝　　だから, c2＝ a2＋b2＝ c2　　a2＋b2 となるから, 　　　　三角形
	(6)	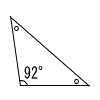三角形

［トップに戻る］ ［前ページに戻る］ ［次ペ−ジに進む］ ［答のペ−ジに進む］