| Ѓi‚UЃj‘ЉҺ—‚МЏШ–ң‚P | ЉwЏK“ъЃ@ Ѓ@ ЊҺЃ@ Ѓ@“ъЃiЃ@Ѓ@Ѓj | |||||||||||
|
||||||||||||
| Ѓi‚UЃj‘ЉҺ—‚МЏШ–ң‚P | ЉwЏK“ъЃ@ Ѓ@ ЊҺЃ@ Ѓ@“ъЃiЃ@Ѓ@Ѓj | |||||||||||
|
||||||||||||
| ‚P | 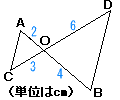 Ѓ@ЃұAOCЃдЃұBOD‚Е‚ ‚йЃB Ѓ@ЃұAOCЃдЃұBOD‚Е‚ ‚йЃBЃmЏШ–ңЃn ЃұAOC‚ЖЃ@Ѓ@Ѓ@Ѓ@‚Й‚Ё‚ұ‚Д
‘ЉҺ—ЏрЊЏ(Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@) Ѓ@Ѓ@Ѓ@‚Ғ‚»‚к‚ә‚к“™‚µ‚ұ‚©‚з, Ѓ@ЃұAOC ЃдЃ@ |
‚Q | 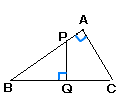 Ѓ@ЃұABCЃдЃұQBP‚Е‚ ‚йЃB Ѓ@ЃұABCЃдЃұQBP‚Е‚ ‚йЃBЃmЏШ–ңЃn ЃұABC‚ЖЃ@Ѓ@Ѓ@Ѓ@‚Й‚Ё‚ұ‚Д
‘ЉҺ—ЏрЊЏ(Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@) Ѓ@Ѓ@Ѓ@‚Ғ‚»‚к‚ә‚к“™‚µ‚ұ‚©‚з, Ѓ@Ѓ@ЃұABC ЃдЃ@ |
||||||||||||
| ‚R | 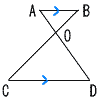 Ѓ@ЃұABOЃдЃұDCO‚Е‚ ‚йЃB Ѓ@ЃұABOЃдЃұDCO‚Е‚ ‚йЃBЃmЏШ–ңЃn Ѓұ‚`BD‚ЖЃ@Ѓ@Ѓ@Ѓ@‚Й‚Ё‚ұ‚Д
‘ЉҺ—ЏрЊЏ(Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@) Ѓ@Ѓ@Ѓ@‚Ғ‚»‚к‚ә‚к“™‚µ‚ұ‚©‚з, Ѓ@Ѓұ‚`BO ЃдЃ@Ѓ@Ѓ@ |
‚S | 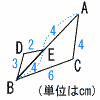 Ѓ@ЃұABCЃдЃұEBD‚Е‚ ‚йЃB Ѓ@ЃұABCЃдЃұEBD‚Е‚ ‚йЃBЃmЏШ–ңЃn Ѓұ‚`BC‚ЖЃ@Ѓ@Ѓ@Ѓ@‚Й‚Ё‚ұ‚Д
‘ЉҺ—ЏрЊЏ(Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@Ѓ@) Ѓ@Ѓ@Ѓ@‚Ғ‚·‚Ч‚Д“™‚µ‚ұ‚©‚з, Ѓ@ЃұABC Ѓд |
||||||||||||
| Ѓmѓgѓbѓv‚Й–Я‚йЃn Ѓm‘OѓyЃ[ѓW‚Й–Я‚йЃn ЃmҺџѓyЃ|ѓW‚Йђi‚ЮЃn Ѓm“љ‚МѓyЃ|ѓW‚Йђi‚ЮЃn |