|
���@���@�R | |||
| 17�@�ΐ쌧�@�`�@24�@�O�d�� |
|
���@���@�R | |||
| 17�@�ΐ쌧�@�`�@24�@�O�d�� |
| 17�ΐ쌧 | �P (1) 7�{2��9 �@ (2) 8�|2��6
�e�ӂ�2�悵��, 82��n��822���, 64��n��67.24 �@�����, n��65, 66, 67 �S 3�~2x�|4�~2x�{5��4 �@6x�|8x��4�|5 �@�|2x���|1���, x�� �T �G �@�A�c2�g�̕����������� �@�C�c2�g�͑S����38�l, �@�@�@�@1�g�͏��Ȃ��Ƃ�2�l�͂͂���37�l�ȉ� �@�E�c1�g��40�_����,2�g��40�_��菬 |
22���� |
�Q �^����(6a�{b)(6a�|b)��(6�~8�{47)(6�~8�|47) �@�@�@��95�~1��95 �R �ڍ�����,x2�|8x�|20��0 �@(x�|10)(x�{2)��0���, x��10,�|2 �@�@�Q�Ԗ��@�`���܂��` 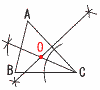 �P �E�} �@���,��C�̓����� �A���,AC�̐��������� �@�@�A�̌�_�����SO
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18���䌧 | �P (1) 8�|18���|10
�Q (a�|b)(x�{y) �R�㎮�{�����~2���,5x��20��,x��4 ������㎮�ɑ������,4�{2y���|2��,y���|3 �S CA����22�{(3��5)2��7cm �T�@�ŕp�l��50�`60���̊K����55�� �@�@�͈́�58�|12��46�� �U 4, 16, 28, �c�Ȃ� �@(4�̏ꍇ) �@�@�A��3������, 2n, 2n�{2, 2n�{4 �Ƃ����, �@�@(2n)2�{(2n�{2)2�{(2n�{4)2�{4 �@�@�@��12(n2�{2n�{2) �� (12�~����)�̌` 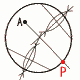 �@�@�����,12�̔{�� �@�@�����,12�̔{���V �E�}(AO�Ɖ~���̌�_) �E���̐�������l��m������ �El��m�̌�_O���Ƃ� �E������AO�Ɖ~���̌�_��P�Ƃ��� |
23���m�� | �P 6�|5��1 �i���C�j �Q 6x�{9�|2x�{6��4x�{15 �i���G)
���̌������,
�@12����1.3x�~1.2��1.56x�l �@12���|10����1.56x�|x��0.56x��2800 �@�����,x��2800��0.56��5000�l�i���E) �U x�|3���|2x�|6���,��_��(�|1,�|4) �@�X��2�ƕ��s������,y��2(x�{1�j�|4��2x�|2 �i���C) 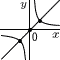 �V (�E�}�Q��) �A,�I �V (�E�}�Q��) �A,�I�W x�Ƃ����,�䗦���,
�X �S6������2���̎��o������6�~5��2��15�ʂ� �@A1����B1���c3�~2��6�ʂ� �@B1����C1���c2�~1��2�ʂ� �@C1����A1���c1�~3���R�ʂ�
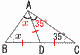
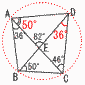 10(�E�}�Q��) 10(�E�}�Q��)�@��DEC��,��D��82�|46��36�� �@��BAC����BDC��36�����, �@�@ �@����ā�DAE����DBC��50���i���G�j |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19�R���� |
�@�@�Q�Ԗ��@�`���܂��` �P �G �@60x�c�����n�߂̓��̂� �@80(10�|x)�c�r������̓��̂� 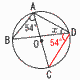 �Q (�E�}�Q��) �Q (�E�}�Q��)�@��BDC����BAC��54��(�~���p) �@��ADC��90��(���a�̉~���p) �@�����,��x��90�|54��36�� �R �E�} 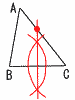 �EBC�̐����ɓ����������� �EBC�̐����ɓ������������EAC�Ƃ̌�_���Ƃ�
|
24�O�d�� | �@�y�@�O�@���@�z �P 9�|2��7 �Q 10x�{45�|x�{7��9x�{52 �R ���ӂ����ւ���, �@a�{b��3m��, a��3m�|b
�T {(x�{1)�|3}2��0���, (x�|2)2��0 �@�����, x��2 �U ��Ꭾ���g����,80:500��x:2250 �@�����, x��80�~2250��500��360g
�@7x�|40��6x�{180 �@�����������,�P�[�L1��, x��220�~ �@�����Ă������z��,7�~220�|40��1500�~ �X ��ʔ��a3cm,����6cm�̉~���� �@�̐ρ� 10 �G, �I, �L 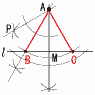 11 �E�} (��ʂ�l ��̐��O�p�`) 11 �E�} (��ʂ�l ��̐��O�p�`)�EA����l �ɐ���AM�����낷 �EAM��1�ӂƂ��鐳�O�p�`AMP������ �E��PAM�̓��������� �El �Ƃ̌�_B���Ƃ� �El ���,BA��BC�ƂȂ�_C���Ƃ� |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20���쌧 | �P 5�|4��1�@�@�Q�@2x�{3�{6x�{2��8x�{5 �R�@�㎮�|�����~3���,y��2 �@����������ɑ������,x�{2�~2��2��,x���|2 �@�����, x���|2, y��2 �S 9�|a���������ɂȂ�悢����, �@�@9�|a��1, 4���, a��5 ,8 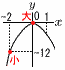 �T ���̌������, �T ���̌������,
�@a��7b�{c��, �C �V (�E��}�Q��) 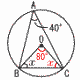 �@x���|2�̂Ƃ�,y���|3�~(�|2)2���|12 �@x���|2�̂Ƃ�,y���|3�~(�|2)2���|12�@x��0�̂Ƃ�,y���|3�~02��0 �@�����, �|12��y��0 �W (2,�|2)��ʂ�o�Ȑ���, �G �X (�E��}�Q��) �@��BOC��40�~2��80�� 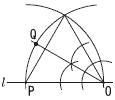 �@��OBC��,��x��(180�|80)��2��50�� �@��OBC��,��x��(180�|80)��2��50��10 �E�}(��) �E1�Ӑ��O�p�`����} �E�E����60��������� �E�������OP��OQ�ƂȂ�Q���Ƃ� 11 (2,6) (3,4) (4,3) (6,2) ��4�ʂ� �@�m����4��36��  12 (�E�\�Q��) 12 (�E�\�Q��)�@�x���v��9��0.15��60�l �@2��̓x����60�~0.25��15�l �@3��̐��k����60�|(9�{24�{15) �@�@��60�|48��12�l [�ʉ�] 3��̑��Γx��0.20 ����v�Z���Ă��悢 |
�y�@��@���@�z �P 7�{2��9 �Q 5x�|2
�@�����x���|8��������,a���|8�|4��4 �T (x�|8)(x�{1) �U 4�{4��6�|��6�|6���|2�{3��6 �V ���̌������,
 �X 2x�{2���|x�{6���,x�� �X 2x�{2���|x�{6���,x��
 11 (�E��}�Q��) �@2x�{35�~2��180���, ��x��55�� 12 �E�} �@���S��,BC�̐����ɓ����� �@�@��B�̓����̌�_ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21�� | �P �|12�{5���|7 �Q �|y���|3x�{4���, y��3x�|4 �R (��6)2�|22��6�|4��2 �S �G �@�A�@y��x2 (2��ɔ��) �@�C�@y��60�|x (1����) �@�E�@y��130x ( ���) �@�G�@y��10/x (�����) �T A��B, B��A �Ƃ���  �@�m���� �@�m�����U (�E�}�Q��) �@��ʂ̉~����4�� �c�A �@���ʂ̌ʁ�12���~ �@�A���C���, x��4�~30��120�� �@�@�Q�Ԗ��@�`���܂��` �P x�{2 �Q x2�{(x�{1)2�{(x�{2)2 �@��x2�{x2�{2x�{1�{x2�{4x�{4��3x2�{6x�{5 �R 3x2�{6x�{5��245���,x2�{2x�|80��0 �@(x�|8)(x�{10)��0��, x��0���, x��8 |
�@ |
| �m�g�b�v�ɖ߂��n�@�m�O�y�[�W�ɖ߂��n�@�m���y�|�W�ɐi���n |