|
正 答 3 | |||
| 17 石川県 ~ 24 三重県 |
|
正 答 3 | |||
| 17 石川県 ~ 24 三重県 |
| 17石川県 | 1 (1) -11 (2) 5-18=-13
2 解の公式より,
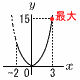
4 (右図参照) x=3のとき,最大値y=15だから, y=ax2に(3,15)を代入して,15=32a よって, a=15/9= 5 条件a+2b=10に合うのは,次の3通り (a,b)=(6,2) (4,3) (2,4) よって,確率=3/36= |
22静岡県 | 1 (1) 9-18=-9 (2) 3a-7b
2 与式=4a2-12a+9-4a2+20a =8a+9=8× 3 x2-9x+8=x-13 移項して整理すると,x2-10x+21=0 (x-3)(x-7)=0より, x=3,7 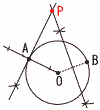 2番問題 ~おまけ~ 1 右図 ・Aを通る接線を引く ・OBの垂直二等分線を引く ・2直線の交点をPとする 2 上から3行目は, 6 14 22 30 38 … よって, 6+8(n-1)=8n-2 3 取り出し方は全部で,6×3=18通り ・A(青か白)B(赤)の確率= ・A(赤か白)B(青)の確率= よって,確率= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18福井県 | 1 (1) 9-12=-3
(3) 6x-9y+2x+12y=8x+3y
2 (a+2)(a-2) 3 上式×2-下式より,9y=-9で,y=-1 これを上式に代入して,x-1=1で,x=2 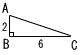 よって, x=2, y=-1 よって, x=2, y=-14 (右図参照) AC=√22+62=√40=2√10cm 5 (1) 32回 (2) 図1 箱ひげ図の中央値は46回だが, 図1の中央値は,50~55回の階級だから, 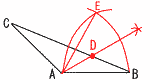 6 右図 6 右図・1辺ABの長さの正三角形 EABを作図する ・∠EABの二等分線を引く ・BCとの交点をDとする |
23愛知県 | 1 -12+2=-10 (答イ)
与式=(x+y)(x-y)+xy=2√3×2√2+1 =4√6+1 (答ウ) 5 移項して,整理すると, x2+x-12=0 (x+4)(x-3)=0より,x=-4,3 (答イ) 6 (答イ)  7 (右図参照) 7 (右図参照)y= 比例定数 a=3×4=12 グラフはy=
右表の6点 (答エ) 8 (答アカ) 9 ヒストグラムより,次の階級を求めると, 最小値は5~10m, 中央値は25~30m 第1四分位数は15~20m これに適する箱ひげ図は (答エ)  10(右図参照) 10(右図参照)△FAB∽△FCE(相似比5:3)より, △BFG∽△BEC(相似比5:8) FG:6=5:8で, FG=6×5÷8= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19山梨県 |
2番問題 ~おまけ~ 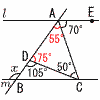 1 解の公式より, 1 解の公式より,
2 (右上図参照) △ADCで,∠D=180-105=75° ∠A=180-(75+50)=55° 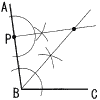 l∥mより,∠x=55+70=125° l∥mより,∠x=55+70=125°3 右図 ・PからABの垂線を引く ・∠Bの二等分線を引く ・2直線の交点が円の中心 4 (右下図参照) 6個 比例定数=(-1)×(-4)=4 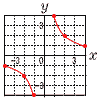 5 5個から2個の取り出し方は, 5 5個から2個の取り出し方は,5×4÷2=10通り
青が含まれる確率 =1-(青が含まれない確率)
|
24三重県 | 【 前 期 】 1 -4+35=31 2 2x+7-3x+2=-x+9
移項して整理すると,x2+x-6=0 (x+3)(x-2)=0より, x=-3,2 5 53, 59
8 半径3cmの半球 表面積=4π×32× 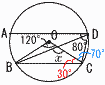 9 (右図参照) 9 (右図参照)△OBCで,∠OCB=30° AD∥BCより,∠OCD=70° ∠BDC=120÷2=60° ∠x=70+60=130° 10 △DBE∽△ABC(相似比3:5) 8:(8+EC)=3:5より,3(8+EC)=40 3EC=40-24で, EC=  11 右図 11 右図∠POA=40°∠A=90° ・二等分線OPを引く ・垂線APを引く ・2直線の交点をPとする |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20長野県 |
4 与式=(x+y)(x-y)=2√5×2√3=4√15 5 (x-5)(x+2)=0より, x=5,-2 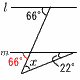 6 (132+x):(12+x)=7:2より, 6 (132+x):(12+x)=7:2より,7(12+x)=2(132+x) 5x=180で, x=36 7 (右図参照) ∠x=66-22=44° 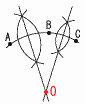 8 右下図 8 右下図・線分ABの垂直二等分線を引く ・線分BCの垂直二等分線を引く ・2本の垂直二等分線の交点がO 9 (1) a, b, c (2) y=3x2にx=2を代入して,B(2,12) 10 並べ方は全部で,3×2×1=6通り 奇数は,123,213,231,321の4通り よって,確率=4/6= 11 ウ 24,26,26,26,28,30,32,34,36,38,40,42,44,48,50 ・四分位数は,Q1=26,Q2=34,Q3=42 ・最小値=24,最大値=50 |
【 後 期 】 1 8-13=-5
3 2x+6y-6x+9y=-4x+15y 4 3・2+2√2√5-5=1+2√10 5 (x-4)(x+3) 6 解の公式より,
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21岐阜県 | 1 8-2=6 2 3x+y-2x+6y=x+7y 3 √3+3√3=4√3 4 y= 10=a/(-6)より,a=-60
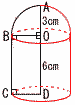 5 イ,エ 5 イ,エ6 (右図参照) 立体=半球+円柱 = =18π+54π=72πcm3 2番問題 ~おまけ~ 1 6x+8 2 (1) 6x+8=7(x-2)より, x=22台 (2) 参加者数は,6×22+8=140人 6人テーブルをy台とすると, 6y+7(22-y)=140 これを解いて, y=14台 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [トップに戻る] [前ページに戻る] [次ペ-ジに進む] |