| 2 |
 a個のみかんを一人5個ずつb人に配ったところ,25個より多く余った。この数量の関係を表した不等式として正しいものを,次のア~工から1つ選び,その記号を書きなさい。 a個のみかんを一人5個ずつb人に配ったところ,25個より多く余った。この数量の関係を表した不等式として正しいものを,次のア~工から1つ選び,その記号を書きなさい。
ア a-5b>25 イ a-5b≧25
ウ a-5b<25 エ a-5b≦25 |
6 |
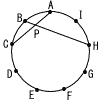 右の図のように,円周を9等分する点を,順にA,B,C,D,E. F,G,H, I とし,点Aと点C,点Bと点Hをそれぞれ結び,その交点をPとする。このとき,∠CPHの大きさは何度か。 右の図のように,円周を9等分する点を,順にA,B,C,D,E. F,G,H, I とし,点Aと点C,点Bと点Hをそれぞれ結び,その交点をPとする。このとき,∠CPHの大きさは何度か。
|
| 3 |
ひかりさんの家から図書館までの道のりは1200mである。ひかりさんは図書館に,分速80mで歩いて向かっていたが,雨が降り出したので,分速200mで走って図書館まで行った。
歩いた時間をa分,走った時間をb分とするとき,bをaの式で表しなさい。
|
7 |
1から5までの数字が1つずつ書かれた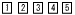 の5枚のカードがある。この5枚のカードを裏返してよく混ぜ,そこから続けて2枚のカードをひく。このとき,1枚目のカードはもとに戻さない。ひいた1枚目のカードに書かれた数字を十の位の数,2枚目のカードに書かれた数字をーの位の数として2けたの整数をつくるとき,その整数が3の倍数ではない確率を求めなさい。ただし,どのカードがひかれることも同様に確からしいとする。 の5枚のカードがある。この5枚のカードを裏返してよく混ぜ,そこから続けて2枚のカードをひく。このとき,1枚目のカードはもとに戻さない。ひいた1枚目のカードに書かれた数字を十の位の数,2枚目のカードに書かれた数字をーの位の数として2けたの整数をつくるとき,その整数が3の倍数ではない確率を求めなさい。ただし,どのカードがひかれることも同様に確からしいとする。
|
 右の図のように,円周を9等分する点を,順にA,B,C,D,E. F,G,H, I とし,点Aと点C,点Bと点Hをそれぞれ結び,その交点をPとする。このとき,∠CPHの大きさは何度か。
右の図のように,円周を9等分する点を,順にA,B,C,D,E. F,G,H, I とし,点Aと点C,点Bと点Hをそれぞれ結び,その交点をPとする。このとき,∠CPHの大きさは何度か。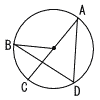 次の図のように,線分ACを直径とする円Oがあり,
次の図のように,線分ACを直径とする円Oがあり,