| １ 番 問 題 |
２番問題 ～おまけ～ |
| １ |
 7×(－2)－(－5)
|
1 |
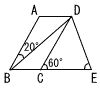  右の図のような,平行四辺形ABCDがあり,∠BADは鈍角である。辺BCをCの方に延長した直線上にBD＝BEとなる点Eをとる。∠ABD＝20°,∠DCE＝60゜であるとき,∠CEDの大きさは何度か。
|
| ２ |
| a＝－3のとき, a2＋ |
15 |
の値を求めよ。 |
| a |
|
| ３ |
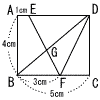
| 4a3b2÷ |
 |
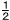ab |
|
２ |
 右の図のような,長方形ABCDがある。辺AD上に2点A,Dと異なる点Eをとり,辺BC上に2点B,Cと異なる点Fをとる。線分EFと対角線BDとの交点をGとする。また,点Dと点Fを結ぶ。
AB＝4cm,BC＝5cm,AE＝1cm,BF＝3cmであるとき,
(ア) 線分DFの長さは何cmか。
(イ) 四角形ABGEの面積は何cm2か。
|
| ４ |
| 連立方程式 |
 |
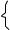3x＋5y＝4 |
を解け。 |
| x－y＝4 |
|
| ５ |
|
| ６ |
(x＋3)2－(x＋3)－30 を因数分解せよ。
|
３ |
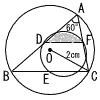  右の図のような,点Oを中心とする半径2cmの円がある。異なる3点A,Ｂ,Cは円周上の点で,∠BAC＝60°である。線分AB,BC,CAの中点をそれぞれD,E,Fとし,3点D,E,Fを通る円をかく。
このとき,点Eを含まない方の弧DFと弦DFで囲まれた部分の面積は何cｍ2か。なお,円周率にはπをそのまま用いよ。
|
| ７ |
次のア～ウの数が,小さい順に左から右に並ぶように,記号ア～ウを用いて書け。
ア －√11 イ 3 ウ －4
|
印刷用