|
正 答 5 | |||
| 33 岡山県 〜 40 福岡県 |
|
正 答 5 | |||
| 33 岡山県 〜 40 福岡県 |
| 33岡山県 | 1 6 2 16+4=20 3 −3a−5−5+3a=−10
5 3−3√3−10=−7−3√3 6 (x−3)2=64 x−3=±8で,x=3±8 x=11,−5となるが, xは正の整数だから, x=11 7 y= 1=a/(−3)で,a=−3 よって, y=− 8 起こらない確率=1−p 9 (正しくないから,反例) a=9のとき,3の倍数だが,6の倍数でない 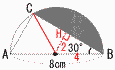 10 (右図参照) 10 (右図参照)扇形OBC=42π× = △OBC= よって, |
38愛媛県 | 1 3+4=7 2 4x−8y+3x+9y−3=7x+y−3
5 (3x2−11x−4)−(x2−6x+9) =2x2−5x−13 〜2番問題 の一部 (おまけ)〜 1 (2x)2−(3y)2=(2x+3y)(2x−3y) 2 両辺を入れ替えて, 3倍して,Sh=3V
ア…3の絶対値は3 イ…m=n=1のとき, m−n=0 ウ…√25=5 4 (右表参照) 和が5か10で,7通り よって, 確率=7/36 5 容積比は,23:53=8:125 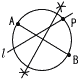 125÷8≒15.6で, 16回 125÷8≒15.6で, 16回6 右図 ・ABを直径とする円をかく ・円とl の交点をPとする |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34広島県 | 1 −8+2+3=−3 2 4x
5 解の公式より,
8 四分位範囲=Q3−Q1だから, A市≒28.3−24.2=4.1 B市≒28.9−24.2=4.7 C市≒34.7−28.7=6.0 D市≒33.3−29.7=4.6 よって, ウ |
39高知県 | 【 A 】 1 (1) −4+12=8
2 23a+7b=14×30 7b=420−23a
ア…長方形は,平行四辺形 4 2b(4a2−9)=2b(2a+3)(2a−3)
これをax+y+10=0に代入して, −4a−2+10=0で, a=2 6 平行でなく,交わらない辺だから, 辺CF,DF,EF 7 順に並び替えると, 2, 2, 3, 4, 4,|6, 7, 8 ,9, 10 四分位数は,Q1=3,Q2=5,Q3=8 最小値=2,最大値=10 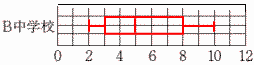 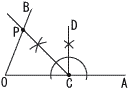 8 右図 8 右図・CからOAの垂線CDを引く ・∠OCDの二等分線を引く ・二等分線とOBの交点 をPとする |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35山口県 | 1 −2
4 3×(−2)+9=−6+9=3 5 6+4√6−5=1+4√6 〜2番問題 (おまけ)〜 1 移項して,(x−2)2=4 x−2=±2で,x=±2−2 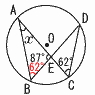 よって, x=4,0 よって, x=4,02 (右図参照) ∠B=∠C=62° △ABEで, ∠x=180−(62+87)=31° 3 (右図参照) 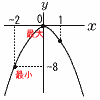 ・x=−2のとき, ・x=−2のとき,y=−2×(−2)2=−8 ・x=0のとき, y=−2×02=0 ・ x=1のとき, y=−2×12=−2 よって, ア(最小値)=−8, イ(最大値)=0 4 10日の階級(60〜80回)で, 最頻値=(60+80)÷2=70回 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36香川県 | 1 3−2=1 2 10−25=−15
=−√2+9 5 x2−2x−3+4=x2−2x+1=(x−1)2 6 x=3を代入すると,−32+3a+21=0 3a=9−21で, a=−4 7 12=22×3だから, 2を2個と,3を1個含むもので, ウ 〜2番問題 (おまけ)〜 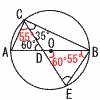 1 (右図参照) 1 (右図参照)∠ACD=90−35=55° ∠ABE=ACD=55° △BDEで, ∠E=180−(60+55)=65° 2 (1) △DGH∽△DEFより, GH:5=9:12で,GH=5×9÷12= (2) △DEFで,DF=√122+52=13cm 高さをhとし,表面積から求める 表面積=底面積×2+側面積 ( 60+30h=240で,h=6 体積=( 3 △ADEで,AE=√52+22=√29cm △AFD∽△ADEより, DF:2=5:√29で,DF=10/√29
|
【 B 】 1 (1) 3−8+4=−1 (2) 27÷9−5=3−5=−2
移項して,3b=660−9a 両辺を3で割って, b=220−3a 3 解の公式より,
−6=a/2で,a=−12 y=− 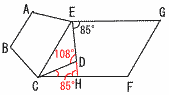 y=(−12)÷(−3)=4 y=(−12)÷(−3)=45 (右図参照) △CDHで, ∠D=108° ∠H=85° ∠DCF=108−85 =23° 6 同色は,白玉か黄玉
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37徳島県 | 1 −8 2 5√3−3√3=2√3 3 因数分解して, (x−7)2=0 x−7=0より, x=7 4 y=axに(−2,10)を代入して, 10=−2aで,a=−5 よって,y=−5x 5 x=2のとき,y= x=6のとき,y=
(赤,青)は,3×1=3通り (白,青)は,2×1=2通り
X−(3a−5b)=−2a+4b X=(−2a+4b)+(3a−5b)=a−b 正しい計算は, X+(3a−5b)=(a−b)+(3a−5b) =4a−6b 8 ∠A+∠B=360−(120+90)=150° 〇+×=150÷2=75° よって,∠x=180−75=105° 9 素因数分解すると, 810=2×34×5 810=3×5×(2×3)×(3×3) =3×5×6×9 よって4数は,3,5,6,9 10 円柱の底面の半径=球の半径=2cm 円柱−球=22π×4−
|
40福岡県 | 1 9−12=−3 2 10a+8b−a+6b=9a+14b
4 x2−x−20−3x+8=0 x2−4x−12=0 (x−6)(x+2)=0より, x=6,−2 5 積が奇数は,AもBも奇数のとき, 積が偶数の確率= よって, 積が偶数の確率=1− 6 x=−1のとき,y=−2×(−1)+7=9 x=4のとき,y=−2×4+7=−1 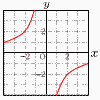 よって, (−1)−9=−10 よって, (−1)−9=−107 右図 8 使用がx人すると,
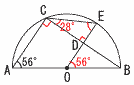 9 (右図参照) 9 (右図参照)△CDEで, ∠C=56÷2=28° ∠D=∠ACB=90° ∠DEC=90−28=62° |
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] |