|
���@���@�S | |||
| 25�@���ꌧ�@�`�@32�@������ |
|
���@���@�S | |||
| 25�@���ꌧ�@�`�@32�@������ |
| 25���ꌧ |
�@������A�ɑ������, �@�@�|4�{y���|1��,y��3 �@�����, x���|2, y��3
�V ��]�́��~���|�~���� �@��32���~4�| �W 4��������,8��10�̕��ρ�9�� �@1 2 3�b3 4 5�b5 6 8�b10 10 12  �X (���`�}�Q��) �X (���`�}�Q��)�@�\���̏o���͑S����8�ʂ� �@���̂���,2���ȏ㗠��4�ʂ� �@�m����4��8�� |
28���Ɍ� | �P �|3�{9��6 �Q �|5y �R 4��3�|2��3��2��3 �S (x�{4)(x�|2) �T y��
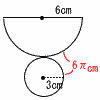 �@�@x���|12��3���|4 �@�@x���|12��3���|4�U (�E�}�Q��) �@ �V (�E���}�Q��) �O�p�`�A��, �@�O�p�̘a��360��������, ��y��360�|(125�{130)��105�� 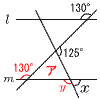 �@��x��180�|105��75�� �@��x��180�|105��75���W 10�`14�x��,4�{11��15�� �@1000�̂���x�Ƃ����
|
||||||||||||||||||||||||||||||||||||||||||||||
| 26���s�{ | �@�y�@�O���@�z �P �|9�~(7�|16)���|9�~(�|9)��81
�@��15��2�|��2�|3��2��11��2 �S ������,�|x�{6y���|1�c�A �㎮�{�A�~2���,9y��3��,y�� ������㎮�ɑ������,2x�|1��5 �@�����, x��3,y��
�U {(2x�{y)�{5}{(2x�{y)�|5} �@��(2x�{y)2�|25 �@��4x2�{4xy�{y2�|25 �V ���̌������,
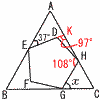 �W (�E�}�Q��) �W (�E�}�Q��)��DHK��,��K��60�{37��97�� �@��H��108�|97��11�� ��HGC��, �@��x��11�{108�|60��59�� �X �~���~���Z�̏�
|
29�ޗnj� | �P (1) 7�{6��13 �@(2) 15�{16��(�|2)��15�|8��7 �@(3) x2�|3x�|10�|2x�{2��x2�|5x�|8 �@(4) ��12�|��27��2��3�|3��3���|��3 �Q �㎮�~4�|�������, �@9y��36��,y��4 �@������㎮�ɑ������, �@�@x�{16��5��,x���|11 �@�����, x���|11,y��4 �R ���̌������,
�S a���|1,b���|1�Ƃ����, �@a�{b���|2, a�|b��0, ab��1, �@�ŏ���, a�{b �T �̐ϔ䁁(������)3������, �@24:B��23:33��,B��24�~27��8��81cm3 �U �\���̏o���͑S����,23��8�ʂ� �@���̂���,�\��2��,����1��� �@�@(�\�\��)�@(�\���\)�@(���\�\) ��3�ʂ� 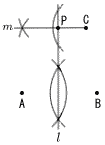 �@�����,�m���� �@�����,�m�����V �E�} �EAB�̐�������l ������ �EC����l �ɐ��������� �El ��m�̌�_��P�Ƃ��� |
||||||||||||||||||||||||||||||||||||||||||||||
| �@�y�@�����@�z �P �|36�{4�~(�|
�@�@��4��3�|12��3���|8��3 �S �㎮�~4�|�����~3���, �@7x��14��,x��2 �@������㎮�ɑ������, �@�@8�{3y���|�V��,y���|5 �@�����, x��2, y���|5 �T xy��5�|9���|4, y�|x���|6��, �@�^����xy(y�|x)��(�|4)�~(�|6)��24
�@�@�@10�� �V (�E�}�Q��) �@��AFG�䁢ABC(������2:5)���, �@�@FG:10��2:5��, FG��4cm �@��DBCG����FBCE��,DG��FE��10cm �@DE��10�{10�|4��16cm �W ���ɕ��ёւ�,4���������, �@�@�@24, 28,�b28, 31,�b33, 35,�b38, 40 �@�l���ʐ���,Q1��28,Q2��32,Q3��37 �@�ŏ��l��24,�ő�l��40  |
30�a�̎R�� | �P (1) �|4
�@(3) 6a�{3b�|a�|5b��5a�|2b
�@(5) a2�{2a�{a2�|2a�|3��2a2�|3 �Q (x�|6)2 �R 0,�}1,�}2,�}3,�}4�� 9�� �S �A��16��200��0.08 �@ �C��24�{56�{64��144 �T y��ax2��(3,�|18)���������, �@�|18��9a��,a���|2 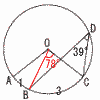 �@�����, y���|2x2 �@�����, y���|2x2�U (�E�}�Q��) �@��BOC��39�~2��78�� �@x:78��4:3���, �@��x��78�~4��3��104�� |
|||||||||||||||||||||||||||||||||||||||||||||||
| 27���{ | �@�y�@A�@�z �P �|20�{127���|13 �Q 3.4�{2.5��5.9�@(59/10����) �R 2�~16��32 �S 8x�|3�{2x�{2��10x�|1 �T �|6y �U ��5�{3��5��4��5 �@�`�Q�Ԗ��̈ꕔ �i���܂��j�` �P �| �Q 4�~(�|3)�{21���|12�{21��9 �R �G �S (2a�{7b)g �@ |
31���挧 |
�@(4) 8x�{4�|6x�|3��2x�{1
�R ���̌������,
�@ x��4�̂Ƃ�,y��2�~42��32
�@ ��ADC��90��(���a�ɑ���~���p) �@�����,��x��90�|40��50�� �U ���o�����͑S����,4�~4��16�ʂ� �a��24�̖ƂȂ�̂�, �@(a,b)��(1,1) (1,2) (2,1) (1,3) (3,1) �@ (2,2) (2,4) (4,2) (3,3) (4,4) ��10�ʂ�
�@n��2�~3�~7��42 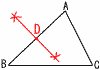 �W (1) �A n�{2�@�C 4 �W (1) �A n�{2�@�C 4�@(2) �E �ǂ��炩����͋��� �X �E�} �EAB�̒��_��D�Ƃ���悢 10 (1) a �C�@�@b �G�@ �@(2) c �E�@�@d �J �@(3) e 1�g�̕ӂƂ��̗��[�̊p |
||||||||||||||||||||||||||||||||||||||||||||||
| �@�y�@B�@�z �P �|6�|16���|22 �Q 10a�{5b�|4a�|12b��6a�|7b
�T (2��5)2�|(��3)2��20�|3��17 �@�`�Q�Ԗ��@�i���܂��j�` �P (�|6)2�|8�~5��36�|40���|4 �Q (x�|2)(x�|9)��0���, x��2,9
�S x��1�̂Ƃ�,y��10�@x��5�̂Ƃ�,y��2
|
32������ | �P 2�|4���|2
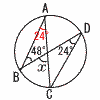 �S 5a�{3b��1000 �S 5a�{3b��1000�T (�E�}�Q��) �@��x��24�{48��72�� �U AB����(3�|1)2�{(5�|2)2 �@�@����4�{9����13 �V �G�@(y��20/x) �W 3���x��,5���y���Ƃ����,
�X (1) a��n�|7 �@(2) b��n�{7,c��n�|1,d��n�{1������, �@�@�^����(n�{7)(n�|1)�|(n�|7)(n�{1) �@�@�@�@��(n2�{6n�|7)�|(n2�|6n�|7) �@�@�@�@��12n �ƂȂ邩��,�@�A |
| �m�g�b�v�ɖ߂��n�@�m�O�y�[�W�ɖ߂��n�@�m���y�|�W�ɐi���n |