全国公立高校入試 　１番問題　【令和５年春】	正　答　３
	17　石川県　〜　24　三重県

17石川県	１ (1) 5＋4＝9 　(2) 9×2−8＝10 　 　(3) 　15x3y2×8 ＝12x2 　2×5xy2 　(4) 　4(4a−2b)−3(3a＋b) 　3×4 　　＝ 16a−8b−9a−3b ＝ 7a−11b 12 12 (5) 3√6−√12÷√2＝3√6−√6＝2√6 ２ y＝に(2,−6)を代入して, 　−6＝a/2で,a＝−12 　よって, y＝− 12 x ３ 根号内が平方数になればよい 　60n＝22×3×5×nより, n＝3×5＝15 ４ a−7b＜200　　(7b＋200＞a等も可) ５ 四分位数を求める (番目) 最小 Q1 (8) Q2 (16) Q3 (24) 最大 四分位 範囲 1　組 2 3 5 7 11 4 2　組 1 3 5 8 10 5 　イ, エ	21岐阜県	和 1 2 3 4 5 6 1 6 2 6 3 6 4 6 5 6 6 12 １ −6＋3＝−3 ２ 　2ab×2 ＝4a 　b ３ 5−2√15＋3＝8−2√15 ４ (右上表参照) 　表より,和が6の倍数は6通り 6の倍数にならない確率 　＝1−6の倍数になる確率 　＝1−6/36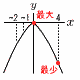＝ ５ (右図参照) イとエ 　ア…xが負のとき,2ずつ増加 　イ…ともに−8≦y≦0 (正) 　ウ…y軸対称 　エ…上に凸 (正) ６ 右図 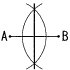・点Aから弧を引く ・点Bから弧を引く ・2つの弧の交点を結ぶ 　〜２番問題 （おまけ）〜 １ Aの底面の1辺＝20÷4＝5cmで, 　面積＝52＝25cm2 ２ Bの他の1辺＝(10−x)cmで, 　面積＝x(10−x)cm, または(10x−x2)cm ３ 40x(10−x)＝25×30 　　4x2−40x＋75＝0 　　(2x−5)(2x−15)＝0より,x＝, 　短辺はcm
18福井県	【　選択Ａ　】 １ (1) −3＋10＝7　　(2) 　4ac×6ab ＝8a2 　3bc 　(3) √12＋√27＝2√3＋3√3＝5√3 　(4) 　3(a＋2b)−2b ＝ 3a＋6b−2b 　2×3 6 　　＝ 3a＋4b 6 ２ (a−3)(a＋2) ３ (1) 上式×3＋下式より, 　　　5x＝10で,x＝2 　　これを上式に代入して, 　　　2−y＝5で,y＝−3 　よって, x＝2,y＝−3 　(2) 解の公式より, 　x＝ −1±√12−4×1×(−1) 2×1 　　＝ −1±√1＋4 ＝ −1±√5 2 2 ４ 50x＋100y＞1000 ５ 最も長い辺は√13cm 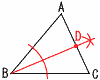　22＋32＝(√13)2 　三平方の定理が成り立つから, ６ 右図	22静岡県	１ (1) −8−3＝−11 　(2) 　36a2×9b ＝27a 　12ab 　(3) 　7(2x＋y)−3(x＋5y) 　3×7 　　＝ 14x＋7y−3x−15y 21 　　＝ 11x−8y 21 　(4) 3√5＋ 　10√5 ＝3√5＋2√5＝5√5 √5√5 ２ 因数分解してから,代入 　(a＋5b)(a−5b)＝(41＋40)（41−40)＝81 ３ x2＋5x−24＝0 　(x＋8)(x−3)＝0より, x＝−8,3 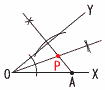　〜２番問題 （おまけ）〜 １ 右図 ・AからOYに垂線を引く ・∠XOYの二等分線を引く ・2直線の交点をPとする ２ a＋bが正の数ならば,aもbも正の数である。 (反例) a＝2,b＝−1のとき, 　a＋b＞0だが,b＜0となる ３ 2枚のカードの取り出し方は全部で 　　　　4×5＝20通り IIがIの倍数となるのは,次の7通り 　(I,II)＝(2,6) (2,8) (2,10) (3,6) (3,9) 　　　　 (4,8) (5,10) よって, 確率＝ 7 20
	【　選択B　】 １ (1) √12＋√27＝2√3＋3√3＝5√3 　(2) 　3(a＋2b)−2b ＝ 3a＋6b−2b 　2×3 6 　　＝ 3a＋4b 6 ２ 502−1＝(50−1)(50＋1)＝72×51 　与式＝√72×51＝7√51 ３ (1) 上式×3＋下式より, 　　　5x＝10で,x＝2 　　これを上式に代入して, 　　　2−y＝5で,y＝−3 　よって, x＝2,y＝−3 　(2) 解の公式より, 　x＝ −1±√12−4×1×(−1) 2×1 　　＝ −1±√1＋4 ＝ −1±√5 2 2 ４ 50x＋100y＞1000 ５ B班の平均値が大きい。 (説明) 　A班の合計時間が30分増加したから, 　　平均値は,30÷10＝3分増加したが, 　　　まだ,5分の差より少ない ６ 最も長い辺は√13cm 　22＋32＝(√13)2 　三平方の定理が成り立つから, 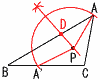７ 右図 点AがBC上の点A'に 　重なるとき,PA＝PA' ∠APA'の二等分線を折り目と 　すればよい ・中心P,半径PAの円をかく ・BCとの交点にA'をとる ・∠APA'の二等分線を引く ABとの交点をDとする
		23愛知県	１ 6−(−2)＝6＋2＝8 （答エ） ２ 　3(3x−2)−2(2x−3) ＝ 9x−6−4x＋6 　18 18 　＝ 5x 　（答ウ） 18 ３ 　6x2×27xy2 ＝18x （答ウ） 　9x2y2 ４ (√5−√2)(2√5＋2√2) 　＝2×5−2×2＝10−4＝6 （答ア） ５ x2−6x＋9＝−x＋15 　x2−5x−6＝0 　(x＋1)(x−6)＝0より,x＝−1,6 （答ウ) ６ （答イ） 　ア…y＝100/x (反比例) 　イ…y＝3x (比例・一次関数) 　ウ…y＝πx2 (2乗に比例) 　エ…y＝x3 (3乗に比例) ７ 1が重なるから,3枚の並べ方は 　　　(4×3×2)÷2＝12通り 　213以上は次の5通り 　　　213, 231 ,311, 312, 321 　よって，確率＝5/12 （答ウ） ８ （答イ） 　4nは偶数だから,4n＋5は奇数 ９ 変化の割合＝ 2×32−2×12 ＝ 18−2 ＝8 3−1 2 　1次関数では,傾きに等しいから （答エ） 10 （答イ,ウ）　 　ア, エ…平面は無数にある(誤)
19山梨県	１ 6＋7＝13 ２ 14×(− )＝−4 ３ −4＋25＝21 ４ 2√2−3×(3√2)＝2√2−9√2＝−7√2 ５ 　9x2y×4x) ＝−x2 　−8xy ６ 3x2＋4x−3x2−27＝4x−27 　〜２番問題の一部 （おまけ）〜 １ (x＋3)(x−12)＝0より, x＝−3,12 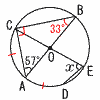２ (右図参照) △ABCで,∠C＝90°より, 　∠B＝90−57＝33° 　∠x＝2∠B＝66° ３ a＝xyに(4,−5)を代入して, 　比例定数＝4×(−5)＝−20 ４ 右図 ・Oからl の垂線を引く ・l との交点をとる	24三重県	【　前　期　】 １ 36−８＝28　　２ 8x−4−6x＝2x−4 ３ 　30ab×5 ＝25a 　6b ４ 3√2− 　4×√2　. ＝3√2−√2＝2√2 2√2×√2 ５ x2−3x−18＝3ｘ−27 　　x2−6x＋9＝0 　　(x−3)2＝0より, x＝3 ６ x＜5y ７ 変化の割合＝ 62a−22a ＝ 32a ＝8a 6−2 4 　8a＝4より, a＝ ８ 表面積＝4π×52＝100πcm2 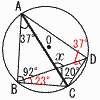９ (右図参照) 　△BCDで, 　　∠D＝37°より,∠B＝23° 　∠ABD＝92−23＝69° 　∠x＝37＋69＝106° 10 下図のいずれか 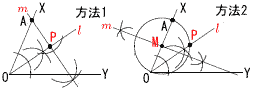[方法1] ・∠XOYの二等分線ｌを引く ・Aからl に垂線mを引く ・l と垂線mの交点をPとする [方法2] ・∠XOYの二等分線l を引く ・OAの垂直二等分線mを引き,中点Mをとる ・OAを直径とする円Mを引く ・l と円Mの交点をPとする 　【　後　期　】 １ 4＋3＝7　　２ 12x−30y ３ 　 5√5 . ＋2√5＝√5＋2√5＝3√5 　√5√5 ４ (x−1)(x−4) ５ 解の公式より, 　x＝ −(−7)±√(−7)2−4×3×1 2×3 　　＝ 7±√49−12 ＝ 7±√37 6 6  ６ 　√40n ＝ 23×5×n 　3 9 　根号内が平方数になればよいから, 　　n＝2×5×9＝90 ７ y＝axに(10,−2）を代入して, 　　−2＝10aより,a＝− 　　y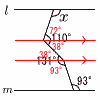＝−xにy＝を代入すると, 　　　＝−xより, x＝×(−5)＝− ８ (右図参照) 　平行線を引き,錯角を求める 　131−93＝38° 　110−38＝72° 　∠x＝180−72＝108° ９ 平行でなく,交わらない辺で,オキク 10 7人の階級4〜6秒で,最頻値＝5秒 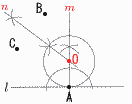11 右図 ・Aからl の垂線mを引く ・BCの垂直二等分線nを引く ・l とmの交点をOとする ・Oを中心に,半径OAの 　　円をかく
20長野県	１ 1　　　２ イ ３ 　2(3x−5y)−(2x−y) ＝ 6x−10y−2x＋y 　4 4 　　＝ 4x−9y 　(x−yも可) 4 ４ x−3＝Xとすると, 　X2＋2X−15＝(X＋5)(X−3) 　　＝(x−3＋5)(x−3−3)＝(x＋2)(x−6) 5 解の公式より, 　x＝−1±√12−1×(−1)＝−1±√2 ６ xy＝12で,yはxに反比例するから, イとウ ７ ウ ８ 5個から2個の取り出し方は全部で, 　　5×4÷2＝10通り 　赤1個,青1個の取り出し方は 　　2×3＝6通り 　よって,確率＝6÷10＝ ９ x＋y＝−1にx＝2を代入して, 　　2＋y＝−1より,y＝−3 　(2,−1）を代入して成り立つのは, エ 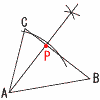10 右図 ・AからBCにの垂線をおろす ・垂線とBCの交点をPとする 11 外角の和は360°より, 　∠x＝360−（90＋56 　　＋80＋70)＝64° 12 Bの高さをhcmとすると, 　22π×h＝π×33 　h＝36π÷4π＝9cm