|
���@���@�P | |||
| �P�@�k�C���@�`�@�W�@��錧 |
|
���@���@�P | |||
| �P�@�k�C���@�`�@�W�@��錧 |
| �P�k�C�� | �P (1) 9�{5��14 �@�@(2) 9�~6��54 �@�@(3) ��28����4�~��7��2��7 �Q ������2,4,6,8��4�ʂ��, �R y��ax�{b��(�|1,6)��(3,2)��������,
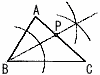
�S ������hcm�Ƃ����, �@h��132����12����11cm �T ��ab��14���,(1,14)��(2,7)��2�ʂ��, �@�����a(a�{b)��15��9 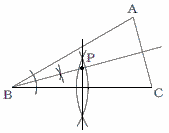 �U �E�} �U �E�}��p15���̓ӎO�p�` PBC����}����悢 �E��B�̓��������� �EBC�̐��������� �@�@���� �E��_��P�Ƃ��� |
�T�R�`�� | �P (1) 1�|2�{5��4
�Q x2�|5x�|14�{9x�{13��0 �@x2�{4x�|1��0 ���̌������,
�@�@���|2�}��4�{1���|2�}��5 �R �^����(x�|y)2��(23�|18)2��52��25 �S �G �@ �Z �c �R�`��19.3��,��c��16.4�� �A �Z �c �R�`��9.2��,�đ��9.5�� �B �~ �c �R�`�ƐV�����قړ�����,8��  �T �C �T �C�@���ʐ}�͐��ʂ��猩���}��, �@�@�C�ł�,�E�̐Ԑ����K�v |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| �Q�X�� | �P (1) �|6�@�@(2) 4�~3�{3��15 �@ (3) 4x2�|2x�{1�@�@(4) 3x�{2y
�R ���Γx����6��20��0.3 �@�ݐϑ��Γx����11��20��0.55 �S �^����3(x2�|2x�|15)��3(x�|5)(x�{3) �T a��4��2��2 �@y��2x�{b��(1,�|3)��������, 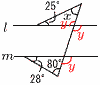 �@�@�|3��2�~1�{b���,b���|5 �@�@�|3��2�~1�{b���,b���|5�U (�E�}�Q��) �@��y��28�{80��108�� �@��x��180�|(25�{108)��47�� �V (�E�}�Q��) 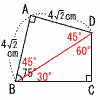 ��ABC�͒��p�ӎO�p�` ��ABC�͒��p�ӎO�p�`�@BD2��(4��2)2�{(4��2)2��64 �@BD��8 ��BCD��30,60,90���̒��p�O�p�` �@BC:8����3:2���,BC��4��3cm �W �E �@���̉��̒������l���ʔ͈� �@�@�@����3�l���ʐ��|��1�l���ʐ� |
�U�{�錧 |
�S �ڍ�����,4a��9b�|3 �@4�Ŋ�����, a��
�@7x��21��,x��3 �@������㎮�ɑ������,3�~3�|y��17 �@�@�|y��17�|9��,y���|8 �@�����, x��3,y���|8
�@y�� �@�����y�� �W �E �A A��2��,B��1��(��) �C A��7�|3��4��,B��7�|4��3��(��) �E B�̒����l��6����,18�l����(��) �G A�͑S����35�l,C�͔�����18�l(��) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| �R�H�c�� |
�S �^����2x�|10y�{10x�{15y��12x�{5y �@��12�~
�@5x��30��, x��6 �V �㎮�~4�{�������,9x��27 �@x��3��,������㎮�ɑ������, �@2�~3�{y��5���,y��5�|6���|1 �@�@�����, x��3, y���|1 �W ���̌������,
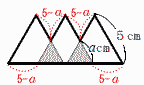 �X (�E�}�Q��) �X (�E�}�Q��)(5�|a)�~6�{5�~3 �@��45�|6a(cm) 10 231��3�~7�~11���, n�{2��231�̖�, 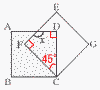 �@n�{2��3,7,11,21,33,77,231 �@n�{2��3,7,11,21,33,77,231�@�@n��1,5,9,19,31,75,229 �f��n��100������, n��5,19,31 11 (�E�}�Q��) ��x��360�|(90�{90�{45�j �@��360�|225��135�� 12 ��BOC��(180�|42)��3��46�� �@��x��46��2��23�� 13 2�p������聢DAC�䁢ABC �@AD:12��6:8��,AD��12�~6��8��9���� 14 (�E�}�Q��)
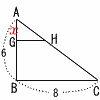 �}2�́�ABC��,AG��x�Ƃ����, �}2�́�ABC��,AG��x�Ƃ����,�@�̐ϔ���,���̂悤�ɂȂ�悢 �@��AGH:��ABC��x2:62��1:3 x2��36��3��12��,x��2��3 �@GB��6�|2��3(cm) 15 �~���̕���̒�����xcm�Ƃ����, �@2��x��8���~3.5��28����,x��14 �\�ʐρ����ʐρ{��ʐ� �@�� |
�V������ |
�P (1) �|3
�@(3) (�|3a)�~(�|8b3)��24ab3 �@(4) 2��2�|3��2���|��2 �Q �̐ϔ䁁(������)3��, 23��8�{ �@�`�Q�Ԗ�� �i���܂��j�`
�Q �ڍ�����,2y���|3x�{4
 �R �E�} �E��B��2������������ �E��AC�Ƃ̌�_��P�Ƃ���
�T �G �q�X�g�O��������l���ʐ������߂� �@Q1��6��,Q2��9��,Q3��13�� �@ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| �S��茧 | �P �|3 �Q 2x�|3x�{y���|x�{��y �R 6�|2��4 �S (x�{4)(x�{6) �T ���̌������,
�@�`�Q�Ԗ�� �i���܂��j�` �����`��1�Ӂ�4a��4��a �@�����,�ʐρ�a2(cm2) �@�`�R�Ԗ�� �i���܂��j�`
�@�܂�O���t��̓_(1,a)�́C �@�@�@�_A(1,1)�������, �G |
�W��錧 | �P (1) �|5 �@(2) 2x�{6y�|5x�{4y���|3x�{10y
�@�`�Q�Ԗ�� �i���܂��j�` �P �C,�G �C ���ׂčŏ��l�Ƃ��Ă� �@�@�@���v�_��31�{20�{22��73�_ �G �p���Q3(19�l��)��81�_��, �@�@�@����ȏ��6�l���� �Q 252��22�~32�~7���, n��7 �R a���|1���������, �@x2�{3�~(�|1)x�{(�|1)2�|7��0 �@x2�|3x�|6��0 ���̌������,
�@30x�{22��35(x�|1)�{32 �@30x�|35x���|35�{32�|22 �@�|5x���|25��,x��5�� |
| �m�g�b�v�ɖ߂��n �@�@�@�@�@�@�@�@�@�@�m���y�|�W�ɐi���n |