|
(31)鳥取県 | 学習日 月 日( ) |
| 1 | (1) | 6 | 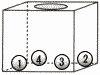 右の図のように,1,2,3,4の数が,それぞれ書かれている玉が1個ずつ箱の中に入っている。この箱から玉を1個取り出し,その玉を箱の中に戻して箱の中をよくかき混ぜた後,もう一度箱から玉を1個取り出す。1回目に取り出した玉に書かれている数をa,2回目に取り出した玉に書かれている数をbとする。 右の図のように,1,2,3,4の数が,それぞれ書かれている玉が1個ずつ箱の中に入っている。この箱から玉を1個取り出し,その玉を箱の中に戻して箱の中をよくかき混ぜた後,もう一度箱から玉を1個取り出す。1回目に取り出した玉に書かれている数をa,2回目に取り出した玉に書かれている数をbとする。このとき,a+bが24の約数である確率を求めなさい。ただし,どの玉が取り出されることも同様に確からしいものとする。 |
|||||
| (2) |
|
|||||||
| (3) | 6√2-√18+√8 |
|||||||
| (4) | 4(2x+1)-3(2x+1) |
|||||||
| (5) | 3xy×2x3y2÷(-x3y) |
7 | 面積が168nm2の正方形の土地がある。この正方形の土地の1辺の長さ(m)が整数となるような最も小さい自然数nの値を求めなさい。 |
|||||
| 2 | ||||||||
| 3 | 二次方程式 3x2-x-1=0 を解きなさい。 |
8 | 連続する2つの偶数の積は,8の倍数である。さよさんは,このことを,次のように文字式を使って証明した。
|
|||||
| 4 | 関数 y=2x2 について,xの値が1から4まで増するときの変化の割合を求めなさい。 |
|||||||
| 5 | 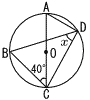 右の図において,∠xの大きさを求めなさい。ただし,4点A,B,C,Dは円Oの周上の点であり,線分ACは円Oの直径である。 右の図において,∠xの大きさを求めなさい。ただし,4点A,B,C,Dは円Oの周上の点であり,線分ACは円Oの直径である。 |
|||||||
| 8 | (1) | 証明の[ア], [イ]にあてはまる適切な数または文字式を入れて,証明を完成させなさい。 ただし,[ア]には,同じ数または同じ文字式があてはまるものとする。 |
10 |
|
||
| (2) | 次の説明は,証明の下線部において,n,n+1が連続する2つの整数だと,n(n+1)は2の倍数となる理由を説明したものである。説明中の[ウ]に適切な文を入れなさい。 説明
|
(1) | 証明の[a],[b]にあてはまるものとして最も適切なものを,次のア~キからそれぞれひとつ選び,記号で答えなさい。 ア 平行線の同位角 イ 平行線の錯角 ウ 平行線の向かい合う辺 エ ∠OAP=∠OCQ オ ∠OPA=∠OQC 力 ∠OBA=∠ODC キ AP=CQ |
|||
| 9 | 図において,△ABCの頂点Cを通り,△ABCの面積を二等分する線分と辺ABとの交点Dを,定規とコンパスを用いて作図しなさい。 ただし,作図に用いた線は明確にして,消さずに残しておき,作図した点Dには記号Dを書き入れなさい。 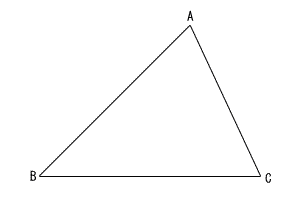 |
(2) | 証明の[c],[d]にあてはまるものとして最も適切なものを,次のア~キからそれぞれひとつ選び,記号で答えなさい。 ア 2組の向かい合う辺は,それぞれ 等しい イ 2組の向かい合う角は,それぞれ 等しい ウ 対角線は,それぞれの中点で交わる エ ∠ABC=∠CDA オ ∠OAP=∠OCQ 力 OA=OC キ AP=CQ |
|||
| 10 | 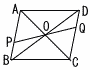 右の図のように,平行四辺形ABCDの対角線の交点Oを通る直線をひき,2辺AB,DCとの交点をそれぞれP,Qとする。 右の図のように,平行四辺形ABCDの対角線の交点Oを通る直線をひき,2辺AB,DCとの交点をそれぞれP,Qとする。このとき,OP=OQであることを,次のように証明した。 |
(3) | 証明の[e]にあてはまる最も適切な語句を入れて,証明を完成させなさい。 |
|||
| [トップに戻る] [前ページに戻る] [次ペ-ジに進む] [答のペ-ジに進む] |