| 【 後 期 】 |
| 1 |
 4-(-3) 4-(-3)
|
9 |
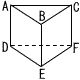 右の図のような,点A,B,C,D,E,Fを頂点とする三角柱があるとき,直線ABとねじれの位置にある直線はどれか,次のア~クから適切なものをすべて選び,その記号を書きなさい。 右の図のような,点A,B,C,D,E,Fを頂点とする三角柱があるとき,直線ABとねじれの位置にある直線はどれか,次のア~クから適切なものをすべて選び,その記号を書きなさい。
ア 直線BC イ 直線CA ウ 直線AD
エ 直線BE オ 直線CF カ 直線DE
キ 直線EF ク 直線FD
|
| 2 |
 6(2x-5y) 6(2x-5y)
|
| 3 |
|
| 4 |
 x2-5x+4 を因数分解しなさい。 x2-5x+4 を因数分解しなさい。
|
10 |
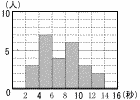 右の図は,P中学校の3年生25人が投げた紙飛行機の滞空時間について調べ,その度数分布表からヒストグラムをつくったものである。例えば,滞空時間が2秒以上4秒未満の人は3人いたことがわかる。 右の図は,P中学校の3年生25人が投げた紙飛行機の滞空時間について調べ,その度数分布表からヒストグラムをつくったものである。例えば,滞空時間が2秒以上4秒未満の人は3人いたことがわかる。
このとき,紙飛行機の滞空時間について,最頻値を求めなさい。
|
| 5 |
二次方程式 3x2-7x+1=0 を解きなさい。
|
| 6 |
うち,もっとも小さい数を求めなさい。
|
11 |
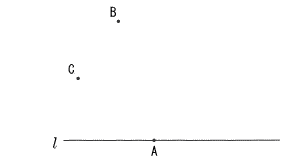
次の図で,直線l と点Aで接する円のうち,中心が2点B,Cから等しい距離にある円を,定規とコンパスを用いて作図しなさい。
なお,作図に用いた線は消さずに残しておきなさい。 |
| 7 |
yはxに比例し,x=10のとき,y=-2である。このとき,y=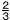 となるxの値を求めなさい。 となるxの値を求めなさい。
|
 |
| 8 |
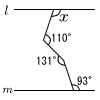 次の図で,2直線l ,mが平行のとき,∠xの大きさを求めなさい。 次の図で,2直線l ,mが平行のとき,∠xの大きさを求めなさい。
|
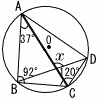 次の図のように,円Oの周上に4点A,B,C,Dがある。
次の図のように,円Oの周上に4点A,B,C,Dがある。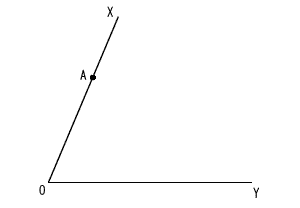
 右の図のような,点A,B,C,D,E,Fを頂点とする三角柱があるとき,直線ABとねじれの位置にある直線はどれか,次のア~クから適切なものをすべて選び,その記号を書きなさい。
右の図のような,点A,B,C,D,E,Fを頂点とする三角柱があるとき,直線ABとねじれの位置にある直線はどれか,次のア~クから適切なものをすべて選び,その記号を書きなさい。 右の図は,P中学校の3年生25人が投げた紙飛行機の滞空時間について調べ,その度数分布表からヒストグラムをつくったものである。例えば,滞空時間が2秒以上4秒未満の人は3人いたことがわかる。
右の図は,P中学校の3年生25人が投げた紙飛行機の滞空時間について調べ,その度数分布表からヒストグラムをつくったものである。例えば,滞空時間が2秒以上4秒未満の人は3人いたことがわかる。
 次の図で,2直線l ,mが平行のとき,∠xの大きさを求めなさい。
次の図で,2直線l ,mが平行のとき,∠xの大きさを求めなさい。