全国公立高校入試 　１番問題　【令和４年春】	正　答　６
	41　佐賀県　〜　47　沖縄県

41佐賀県	１ (1) −8 　(2) −8x＋4y＋5x−2y＝−3x＋2y 　(3) 7xy 　(4) 3√6−2√6＝√6 ２ (x−6)(x＋1) ３ 解の公式より, 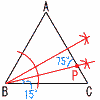　x＝ −(−7)±√(−7)2−4×1×8 2×1 　　＝ 7±√49−32 ＝ 7±√17 2 2 ４ 半径2cmの球＝×23π＝πcm3 ５ 右図 △ABPで,∠ABP＝45° 　つまり,∠PBC＝15° ・∠Bを二等分し, 　さらに二等分すればよい ６ OとCを結ぶ ∠BOC＝2∠A＝50°…ア ∠COD＝2∠E＝30°…イ ア＋イより,∠BOD＝50＋30＝80° ７ データを4分割して, 4,6,6,6,|8,10,12,14,16,18,20,|22,24,28, 30 最小値＝4,最大値＝30 第1四分位数＝7, 第1四分位数＝21 　よって, �A	44熊本県	１ 0.35　　２ −9＋2＝−7 ３ 　2(x＋3y)＋(7x−5y) ＝ 2x＋6y＋7x−5y 　8 8 　＝ 9x＋y 8 ４ 　6ab×3a2b ＝−2a 　−9a2b2 ５ 4x2−12x＋9−4x2＋4x＝−8x＋9 ６ 3√2＋2√3−2√3−2√2＋3√2＝4√2 　〜２番問題 （おまけ）〜 １ 3x＋2x＝8＋7で,5x＝15より,x＝3 ２ 解の公式より, 　x＝ −7±√72−4×2×1 ＝ −7±√41 2×2 4 ３ (1) 7・8番目の平均で, 　　　　(12＋14)÷2＝13m (2) 右図 8,10,10,11,11,12,12,|14,14,15,16,17,17,18 　m＝8　Q1＝11　Q2＝13　Q3＝16　M＝18 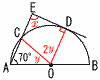４ (右図参照) △OACで,y＝180−70×2＝40° OAEDで,x＋70＋3y＋90＝360 　x＝∠CED＝80°
42長崎県	【　後期　】 １ 5−12＝−7 ２ 3＋2√3＋1− 　6√3 ＝4 √3√3 ３ 2x2−2x−3＝x2 　x2−2x−3＝0 　(x−3)(x＋1)＝0より, x＝3,−1 ４ a＝5b＋3 ５ y＝に(2,6)を代入して, 　6＝a/2より,a＝12 よって, y＝ ６ �B ７ 比率から推定する はじめの当たりくじをx本とすると, 　当たり ＝ 　x　. ＝ 4 　全体 1000 50 x＝1000×4÷50＝80 　およそ80本 ８ 二等辺三角形だから, ∠x＝180−36×2＝108° ９ (右図参照) 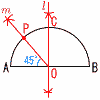×22π×3＝4πcm3 10 右図 ∠POA＝45°になれ 　ばよいから,角を続けて 　　2回二等分する ・ABの垂直二等分線lを引く ・∠AOCの二等分線mを引く ・とmの交点をPとする	45宮崎県	１ −4＋8＝4　２ 　　3×6　. ＝ 18 ＝− 9 　8×(−1) -8 4 ３ 3a−6b−4a＋12b＝−a＋6b ４ 3＋2√6＋2＝5＋2√6 ５ x2−5x−6＝0 　(x−6)(x＋1)＝0より, x＝6,−1 ６ 外角の和は360°だから, 　180−360÷10＝180−36＝144° 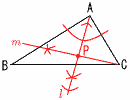７ ウ ８ 右図 ・∠Aの二等分線l を引く ・Cからl に垂線mを引く ・l とmの交点をPとする
		46鹿児島県	１ (1) 32−5＝27 　(2) 　1 ＋ 7×3 ＝ 1 ＋ 1 ＝ 3＋2 ＝ 　2 9×7 2 3 6 　(3) 6−2＝4 　(4) 1〜99では,99÷3−33個 　　　1〜9では,9÷3−3個 　　よって, 33−3−30個 　(5) 相似比が1:2だから,体積比は13:23＝1:8 　　よって, 8倍 ２ 2b＝3a＋5 　b＝ 3a＋5 2 積 6 7 8 9 2 12 14 16 18 4 24 28 32 36 6 36 42 48 54 ３ (右表参照) 積aｂが平方数であればよい 　条件にあうは表の3通り 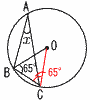よって, 確率＝ 3 ＝ 12 ４ (右図参照) △OBCは底角∠B＝∠C＝65° 　　の二等辺三角形 頂角∠BOC＝180−65×2＝50° よって, ∠x＝50÷2＝25° ５ 　11092×0.49 ＝ 11092 × 49 　5151×0.13 5151 13 　　≒2×4＝8倍　　よって, ウ
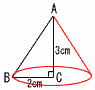
43大分県	１ (1) −13 　(2) 7＋3×(−4)＝7−12＝−5 　(3) 　3(x−y)＋4(x＋2y) 　4×3 　　＝ 3x−3y＋4x＋8y ＝ 7x＋5y 12 12 (4) 　4x2×(−9y) ＝−6x 　6xy (5) 2√6− 2√3√2 ＝2√6−√6 ＝√6 √2√2 ２ 解の公式より, 　x＝ −3±√32−4×1×(−5) 2×1 　　＝ −3±√9＋20 ＝ −3±√29 2 2 ３ 先に因数分解してから,代入 与式＝(x−2)(x−6) 　＝(√7＋4−2)(√7＋4−6) 　＝(√7＋2)(√7−2)＝7−4＝3 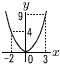４ (右図参照) 最小値はx＝0のときで,y＝0 最大値はx＝3のときで, 　y＝32＝9 よって, 0≦y≦9 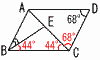５ (右図参照) △ACDは二等辺三角形 　∠ACD＝∠D＝68° ∠D＋∠BCD＝180° 　∠ACB＝112° △EBCも二等辺三角形 　∠EBC＝∠ECB＝112−68＝44° ∠ABE＝∠ABC−44＝68−44＝24° 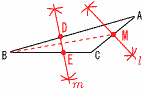６ 右図 ・辺ACの中点M 　をとる ・中線BMの垂直 　二等分線mを引く ・mとABの交点をD,mとBCの交点をEとする	47沖縄県	１ 4−8＝−4 ２ 10×(−)＝−2×4＝−8 ３ 4−6＝−2 ４ 3√2＋2√2＝5√2 ５ 2a×9a2＝18a3 ６ 2x＋10y＋3x−3y＝5x＋7y 　〜２番問題 （おまけ）〜 １ 8x＝3×40＝120で, x＝15 ２ イ ３ ウ ４ ∠D＝∠C＝30° 　∠x＝80−30＝50° ５ 4x2＋4xy＋y2 ６ (x＋6)(x−1)

［トップに戻る］　［前ページに戻る］