全国公立高校入試 　１番問題　【令和４年春】	正　答　３
	17　石川県　〜　24　三重県

17石川県	１ (1) −3　　(2) −3−16＝−19 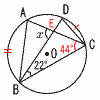　(3) 　6a2b3×5 ＝10ab 　3ab2 　(4) 　4(x＋2y)−5（x＋3y） 　5×4 　　＝ 4x＋8y−5x−15y 20 　　＝ −x−7y 　または, − x＋7y 　20 20 　(5) 2√3＋ 2√6 ＝2√3＋√3＝3√3 2√2 ２ 解の公式より, 　x＝ −(−5)±√(−5)2−4×2×(−1) 2×2 　　＝ 5±√25＋8 ＝ 5±√33 4 4 ３ (右図参照) 円周角は 　弧の長さに比例するから, 　∠CBD＝22×2＝44° ∠xは△EBCの外角で, ∠x＝22＋44＝66° ４ 変化の割合＝ (a＋3)2−a2 ＝13 (a＋3)−a 　6a＋9 ＝13より,6a＋9＝39で,a＝5 　3 ５ 6番目と7番目がともに2回で, 　ア＋イ＝5 となるのは, (ア,イ)＝(2,3) (3,2) (4,1) (5,0)の 4通り 　〜２番問題 （おまけ）〜 １ 100円の比率＝ 　 27　. ＝ 27 ＝ 9 27＋21 48 16 よって,320×＝180枚 ２ 確率＝ 表にまとめると,条件に適するのは3通り 100円 〇 〇 〇 〇 × × × × 50円 〇 〇 × × 〇 〇 × × 50円 〇 × 〇 × 〇 × 〇 × a−b 200 100 100 　0 　0 -100 -100 -200 　（ 〇は表 ×は裏 ）	22静岡県	１ (1) 6−24＝−18 　(2) 　8a2b ＋ 36ab2 ＝2a＋９b 　4ab 4ab 　 　(3) 　2(4x＋y)−5(x−y) 　5×2 　　＝ 8x＋2y−5x＋5y 10 　　＝ 3x＋7y 10 　(4) 9√7−√7・√7√3−3√3 　　＝9√7−7√3−3√3＝9√7−10√3 ２ 先に展開してから,代入 与式＝a2−11a＋30−a2−3a＝−14a＋30 　　＝−14×＋30＝−4＋30＝26 ３ 両辺の平方根をとると, x−2＝±4 　x＝2±4で, x＝6,−2 　〜２番問題 （おまけ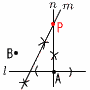）〜 １ 右図 ・線分ABの垂直二等分線m 　を引く ・Aからl と垂直な直線nを引く ・mとnの交点をPとする ２ 4L＝4000ｍL (単位に注意！) 　y＝ 4000 x ３ 6個から2個取り出す方法は全部で 　　　　6×5÷2＝15通り 和が正となるのは,,次の4通り 　　(−1,2) (0,1) (0,2) (1,2) よって, 確率＝ 4 15
18福井県	【　選択Ａ　】 １ (1) 7＋15＝22 　(2) 　12xy×(−3x) ＝−6x2 　6y 　(3) 　2×2a−3(a−b) ＝ a＋3b 　3×2 6 ２ (a−3)(a−5) ３ 解の公式より, 　x＝ −3±√32−4×3×(−1) 2×3 　　＝ −3±√9＋12 ＝ −3±√21 6 6 ４ ア,ウ ５ (右図参照) 2通り 残りの1辺をxcmとすると, 　x＝√49−25＝2√6cm 　x＝√49＋25＝√74cm 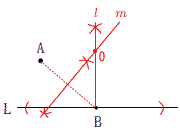６ 右図 ・Bから垂線l 　を引く ・ABの垂直二　　等分線mを 　引く ・lとmの交点を 　中心Oとする 　【　選択B　】 １ (1) 　12xy×(−3x) ＝−6x2 　6y 　(2) 　2×2a−3(a−b) ＝ a＋3b 　3×2 6 ２ 3a(x2＋4x＋3)＝3a(x＋1)(x＋3) ３ 選択Ａの３と同じ ４ 千と一位をa,百と十位をbとすると, 4桁の整数＝1000a＋100b＋10b＋a 　＝1001a＋110b＝11(91a＋10b) 91a＋10bは整数だから,11の倍数となる ５ 選択Ａの５と同じ ６ 平均値＝(2+4+1+…+a+b)÷10＝3より, 　a＋b＝5で,(a,b)＝(0,5) (1,4) (2,3) これらを当てはめて順に並べると, 　0 1 1 2 2 4 4 5 5 6 (中央値は3) 　1 1 1 2 2 4 4 4 5 6 (中央値は3) 　1 1 2 2 2 3 4 4 5 6 (中央値は2.5) よって,(a,b)＝(0,5) (1,4) ７ 選択Ａの６と同じ	23愛知県	【　Ａ　】 １ 8−6＝2 ２ 　3(2x−3)−2(3x−2) ＝ 6x−9−6x＋4 　18 18 　＝− 5 18 ３ 　5x2×32xy2 ＝10x 　16x2y2 ４ (√5−√3)×(2√5＋2√3) 　＝(√5−√3)×2(√5＋√3) 　＝2(√5−√3)(√5＋√3)＝2(5−3)＝4 ５ 10−5x＝x2−2x−18 　x2＋3x−18＝ 　(x＋6)(x−3)＝0より, x＝−6,3 ６ それぞれの式を求めると, ア y＝x3 (3乗に比例) イ y＝ 35 　(反比例) x ウ y＝4x (比例) エ y＝ 15 　(反比例) x 　よって, イ,エ ７ 平均値＝(1＋3＋5＋a＋10＋12)÷6 　　　＝ a＋31 …ア 6 　中央値＝ 5＋a …イ 2 ア＝イより, a＋31 ＝ 5＋a 6 2 　2(a＋31)＝6(5＋a）で, a＝8 ８ A(−3,9) B(6,36)より, 傾き＝ 　36−9 . ＝ 27 ＝3 6−(−3) 9 原点を通るから式は, y＝3x ９ 円柱Pと円柱Qで, 　半径を3kと5k, 高さをh1とh2とすると, (3k)2πh1＝ (5k)2πh2 　約分すると, 9h1＝25h2 よって, h2 ＝ 9 倍 h1 25 10 △ADE∽△CBEより, 3:7＝6:BC 　BC＝7×6÷3−14cm
19山梨県	１ −8 ２ − ＋ ＝ ３ 36−9＝27 ４ 7√3− 　9√3 . ＝7√3−3√3＝4√3 √3√3 ５ 　xy×(−18x) ＝−3x2y 　6 ６ 14x−7y−x＋5y＝13x−2y 　〜２番問題 （おまけ）〜 １ 解の公式より, 　x＝ −9±√92−4×2×8 2×2 　　＝ −9±√81−64 ＝ −9±√17 4 4 ２ 弧AC(Bを含まない側)で考える ∠x＝232÷2＝116° 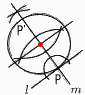３ 右図 ・Pからl の垂線mを引く ・mと円の交点P'をとる ・PP'の中点が中心 ４ それぞれの式は, ア y＝x(比例)　 イ y＝50/x(反比例) ウ y＝3x(比例)　エ y＝0.8x(比例) 　よって, イ ５ 目の出方は全部で,6×6＝36通り 積が10,20,30となるのは次の6通り 　(大,小)＝(2,5) (5,2) (4,5) (5,4) 　　 (5,6) (6,5) よって, 確率＝ 6 ＝ 36
			【　B　】 １ −3＋7＝4 ２ 12x−16y＋15y−12x＝−y ３ x2＋3x−10−3x＋9＝x2−1 　　＝(x＋1)(x−1) ４ (5＋2√10＋2)−(5−2√10＋2) 　　＝(7＋2√10)−(7−2√10)＝4√10 ５ 4x2＋4x＋1−3x2−9x＝x2−5x＋1＝0 ６ y＞3x ７ 6の約数は,1,2,3,4の4個 　よって, 確率＝ ８ y＝ax＋bに,(−3,−8) (1,4)を代入して, 　 −3a＋b＝−8 　　a＋b＝4 これを解いて,a＝3,b＝1 　直線の式は,y＝3x＋1で, これにx＝3を代入すると, y＝3×3＋1＝10 ９ それぞれの体積を計算すると, ア 13＝1 イ ×22×1＝ (約1.33) ウ ×12π×1＝π (約1.05) エ ()2π×1＝π (約0.79) 　よって最大は, イ
20長野県	１ 5−2＝3 ２ −2x＋3 ３ √84n＝2√21√nより, n＝21 ４ 移項すると,x2−x＝0 　x(x−1)＝0より,x＝0,1　よって, ウ 5 エ ６ 中央値は8・9番目 　(15＋19)÷2＝17分 ７ 1−＝ ８ √4＜√6＜√9より,2＜√6＜3 　√6＝2.***だから,a＝√6−2 これを代入して, 　a(a＋2)＝(√6−2)(√6−2＋2) 　　＝(√6−2)×√6＝6−2√6 ９ y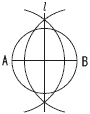＝に(1500,60)を代入すると, 　60＝ 　a　. で,a＝60×1500＝90000 1500 　y＝ 90000 にx＝600を代入すると, x 　y＝90000÷600＝150秒＝2分30秒 10 右図 ・ABの垂直二等分線 　をとる 11 (1)∠x＝120÷2＝60° (2) 62π× 120 360 ＝36π×＝12πcm2	24三重県	【　前　期　】 １ −9−８＝−17 ２ 4x＋5−x＋3＝3x＋8 ３ 両辺を入れ替えると, 　a＋b ＝c 　5 　両辺を5倍して, a＋b＝5c 　aを移項して, b＝5c−a ４ 上式を下式に代入して, 　4x＋5(x−3)＝30 　9x−15＝30より,x＝5 　これを上式に代入して,y＝5−3＝2 よって, x＝5,y＝2 ５ 2√3＋ 1×√3 ＝2√3＋ √3＝ √3 √3√3 ６ x2＋4x＋4＝4x＋13 　x2−9＝0 　(x＋3)(x−3)＝0より, x＝±3 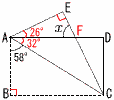７ x＝−6のとき, y＝ 12 ＝−2 −6 　 x＝−3のとき, y＝ 12 ＝−4 −3 変化の割合＝ (−4)−(−2) ＝ −4＋2 ＝− (−3)−(−6) −3＋6 ８ 体積＝π×33＝36πcm3 ９ (右図参照) ∠BAD＝90°より, 　∠CAD＝90−58＝32° ∠CAE＝∠CAB＝58°より, 　∠EAD＝58−32＝26° △EAFで,∠x＝90−26＝64° 10 右図 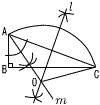△OABが,頂角110°で底角35°の 　二等辺三角形になればよい ・弦ACの垂直二等分線上に中心 　　があるから, 　ACの垂直二等分線l を引く ・∠OAC(底角)＝35°になれば 　　よいから,∠BACの二等分線mを引く ・OとCを結び, 　　l とmの交点Oを中心に弧ACをかく 　【　後　期　】 １ −56　　２ 　12−10 x＝ 2 x　　３ 3y 　5×3 15 ４ 10a＋5b−6a−8b＝4a−3b ５ 6−√21±4√21−14＝3√21−8 ６ y＝に(−2,8)を代入すると, 　8＝ 　a . より,a＝−16 −2 よって, y＝− 16 x ７ 解の公式より, 　x＝ −5±√52−4×2×(−2) 2×2 　　＝ −5±√25＋16 ＝ −5±√41 4 4 ８ (ｳ)≦0.80より, (ｲ)≦0.80−0.65＝0.15 　(ｱ)は, 20×0.15＝3以下 　　すなわち, 0,1,2,3人
21岐阜県	１ 6＋8＝14 ２ −3x＋3y−2x＋y＝−5x＋4y ３ 与式＝(x＋y)2＝(5＋√3＋5−√3)2 　　　＝102＝100 ４ 目の出方は全部で,6×6＝36通り 積が5の倍数となるのは 　(1,5) (2,5) (3,5) (4,5) (6,5) とその逆, 　　ならびに(5,5) の11通り よって, 確率＝ 11 36 ５ 上式＋下式×2より,11x＝22で,x＝2 　これを上式に代入して, 　　10＋2y＝4で,y＝−3 よって, x＝2, y＝−3 ６ 1辺6cmの正三角形の高さは3√3cm 体積＝×62×3√3＝36√3cm3 　〜２番問題 （おまけ）〜 １ a＝−1を代入して, 　x2−x−8＝0 解の公式より, 　x＝ −(−1)±√(−1)2−4×1×(−8) 2×1 　　＝ 1±√1＋32 ＝ 1±√33 2 2 ２ (1) x＝1を代入すると, 　1＋a−8＝0で, a＝7 (2) x2＋7x−8＝0 　(x＋8)(x−1)＝0より, x＝−8