|
���@���@�Q | |||
| �X�@�Ȗ،��@�`�@16�@�x�R�� |
|
���@���@�Q | |||
| �X�@�Ȗ،��@�`�@16�@�x�R�� |
| �X�Ȗ،� | �P �|2
�S ���̌������,
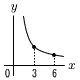 �T (�E�}�Q��) �T (�E�}�Q��)
�@��OBC�͓ӎO�p�`������, �@�@��x��(180�|58)��2��61�� �W ���������ɓ��Ă͂܂�Ȃ�����, �E �@�A 3�ӑ����@�C 2�Ӛ�p���� �@�G 1�ӗ��[�p���� �@ |
13�����s | �P 1�|36�~
�S 5x�|9x���|27�{7 �@�@�|4x���|20���, x��5 �T �㎮�������ɑ�������, 2(4y�{1)�|5y��8 �@8y�|5y��8�|2��,y��2 ������㎮�ɑ������,x��4�~2�{1��9 �����, x��9,y��2 �U ���̌������,
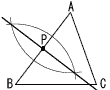 �V �����l��13�l�ڂ�, 4�� �V �����l��13�l�ڂ�, 4���W �ʂ̔���, ��B�� ��DEB��, ��x��34�{17��51�� �X �E�} �EAB�̒��_��P���Ƃ� |
||||||||||||||||||||||||||||||||||||||||||||||||
| 10�Q�n�� | �y�O���z �P (1) 1�{4��5�@(2) 8a�@(3) �|2x2 �@(4) 3x�{3y�|4x�{4y���|x�{7y �@(5) 4ab
�R �㎮�|�������,3y��12��,y��4 ������㎮�ɑ��,x�{4���|1��,x���|5 �@�����, x���|5,y��4 �S �e �T (x�{4)(x�|3)��0���, x���|4,3 �U y��3(x�|2)�{4 �@y��3x�|2 �V BC����62�|42����20��2��5 ��ABC�� |
14�_�ސ쌧 | �A �|6�|9���|15�i���P�j
�I (x2�|7x�{10)�|(x2�|6x�{9) �@�@���|x�{1�i���R�j �@�`�Q�Ԗ�� �i���܂��j
�@������@�ɑ������,x�{16��5��,x���|11 �����, x���|11,y��4 �C ���̌������,
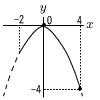 �E (�E�}�Q��)�@�i���Q�j �E (�E�}�Q��)�@�i���Q�j�ŏ��l��x��4�̂Ƃ���, �@a���| �ő�l��x��0�̂Ƃ���, �@b���| �G A�ǂ�x�l�Ƃ����,B�ǂ�(x�|5)�l �@3x��4(x�|5)�{3 �@�����������, x��17�l�i���R�j �I ��Ɉ����������Ă��������� �^����xy(x�{y)��(6�|3)(2��6)��6��6�i���S�j |
||||||||||||||||||||||||||||||||||||||||||||||||
| �y����z �P (1) �|4�@(2) 5x�|2�@(3) 3b2 �Q (1) 4x�|x���|1�|5 �@�@�@3x���|6��,x���|2 �@�@(2) ���̌������,
�S ��Ɍv�Z���Ă���,��� �^����a�|3b��3�|3�~ �T ��p��180�|114��66�� �ځ�180�|66�~2��48�� �U y��ax2��(�|2,8)���������, �@8��a�~(�|2)2���,a��2 y��2x2��x��3���������, �@y��2�~32��18 �V �F�̏o���͑S����,3�~3��9�ʂ� 1���ԋʂ��o��̂�,����4�ʂ� �@(1���,2���) �@�� (��,��) (��,��) (��,��) (��,��) �����, �m���� �W �E �X �E �A 30�~(0�{0�{0.20)��6�l (��) �C A��30�~0.30��9�l B��40�~0.30��12�l(��) �E A��0.10�{0.10��0.20�@B��0.20�{0.15��0.35 �G 30�`35m��,A��3�l,B��6�l���邪, �@�@�N���ō��l���s�� (��) |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| 11��ʌ� | �P �|2x�@�@�Q �|15�{2���|13
�V �㎮�{�����~3���, �@17x��17��,x��1 �@����������ɑ������, �@�@3�{2y���|1��,y���|2 �����, x��1,y���|2 �W ���̌������,
�@��x��220��2��110�� 10 �����̌X���͉E�������,a��0 �@�ؕЂ͐���,b��0 �@�Ȑ��͑�2�E4�ی���,c��0 �����, �J 11 ��AB����ʂ̉~����6�� �@��`�̔��a��8cm������,
�@n��540,135,60,15�� 4�ʂ� 13 ��ABE�䁢DCE���,AE:DE��2:3 ��EBF�䁢CBD���,EF:CD��EF:3��2:5 �@EF��3�~2��5�� 14 �E 15 ���̑�����x�C�Ƃ����,�䗦���
16 �̐ϔ�S:M��33:43��27:64 �@���i��S:M��1:2��,M�������c�A ��ʐϔ�M:L��42:52��16:25 �@�����̔�1:2������, �@�̐ϔ�M:L��16:25�~2��16:50 �@���i��M:L��1:3��,L�������c�C �A�C���,�ł������� L�T�C�Y |
15�V���� | �P 7�|11���|4 �Q 3a�|9b�{4a�|8b��7a�|17b
�S 2��18�|5��2��2�E3��2�|5��2����2 �T ���ӂ�������������, (x�|6)(x�{1)��0 �@�����, x��6,�|1 �U 2�_�̍��W��������,�A�������������� y��ax�{b�� (�|1,1) (2,7) ��������,
������A�ɑ������,�|2�{b��1��,b��3 �@�����, y��2x�{3 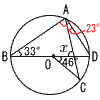 �V (�E�}�Q��) �V (�E�}�Q��)BD�͒��a������, �@�@��BAD��90���c�A ��CAD����COD��2 �@�@��46��2��23���c�C �A�|�C���,��BAC��90�|23��67�� �@�����, x��180�|(33�{67)��80�� �W�@�E,�I �A A�g�̍ő��24m��,30m����͂��Ȃ� �C A�g��24�|11��13m, �@B�g��23�|14��9����,A�g�̕����傫�� �E B�g��36�|7��28m, C�g��33�|9��24m��, �@�@�@������ �G 11�`15����15�`24m�� �@15�`20m�ɏW�܂��Ă��邩�͕s�� �I ��3�l���ʐ�(27�Ԗځj��23m������, �@25m�܂łɂ�27�l�ȏア��̂�,������ �@ |
||||||||||||||||||||||||||||||||||||||||||||||||
| 12��t�� | �P (1) �|6�{2���|4 �@ (2) 4a�|9b�|a�{3b��3a�|6b �@ (3) 12�|4��3�{1��13�|4��3 �Q (1) �c��,2x�{3 �@�@�@�@�ʐς�, x(2x�{3)cm2 �@�@�@�@�@�@�܂���, 2x2�{3x cm2 �@ (2) 2x2�{3x��7��, 2x2�{3x�|7��0 �@���̌������,
�@�@�@3,7,7,9,11,12,14,16 �@�����l��(9�{119��2��10�� (2) ���Ђ��}���, �@�@�����l��9��ɂȂ�悢����, �@�@�@3,7,7a,9,11,12,14,16 �@�@�܂�,7��a��9�@�����,a��7,8,9 �S (1) 2,3,5,7,11,13,17,19�� 8�� �@ (2) �ڂ̏o���͑S����,6�~6��36�ʂ� �@�@2a�{b���f���ɂȂ�͎̂���13�ʂ� �@(a,b)��(1,1) (1,3) (1,5) (2,1) (2,3) �@�@�@�@�@(3,1) (3,5) (4,3) (4,5) (5,1) �@�@�@�@�@ (5,3) (6,1) (6,5)
������C�ɑ������, �@2b�|(�|5)���|1��,2b���|6 �����, a���|5,b���|3 �U (1) ���ӂ����ւ����,
�@���l�p��������h�Ƃ����,
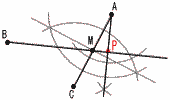 �V �E�} �V �E�}�EAC�̒��_M �@���Ƃ� �E����BM���Ƃ� �EA����BM�� �@���������낷 |
16�x�R�� | �P 3�{10��13
�S 10a�|2b�|9a�{6b��a�{4b �T �������㎮�ɑ������, �@x�{3(2x�|9)��1 �@ x�{6x�|27��1 �@�@�@�@�@7x��28��, x��4 �@����������ɑ������, �@�@y��2�~4�|9���|1 �@�����, x��4, y���|1 �U ���ӂ�������������, �@(x�|9)(x�{2)��0 �@�����, x��9,�|2  �V 2a�{3b��1000 �V 2a�{3b��1000�W (�E�̎��`�}�Q��) �]���ۂ̊m��(�N����Ȃ��m��)�� �@���p����悢 (���Ȃ��Ƃ�1���͕\���o��)�̊m�� �@��1�|(3���Ƃ������o��)�̊m�� �@��1�| 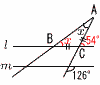 �X (�E�}�Q��) ��ABC��, �@��A����B����x �@��C�̊O�p��180�|126��54�� ��A�{��B����C�̊O�p������, �@��x�{��x��54��, ��x��27�� 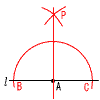 10 �E�} 10 �E�}�E�_A����,AB��AC�ƂȂ� �@�@�_B,C���Ƃ� �E�_A��B����,BP��CP�ƂȂ� �@�@�_P���Ƃ� �E�_P�Ɠ_A������ |
| �m�g�b�v�ɖ߂��n�@�m�O�y�[�W�ɖ߂��n�@�m���y�|�W�ɐi���n |