全国公立高校入試 　１番問題　【令和４年春】	正　答　１
	１　北海道　〜　８　茨城県

１北海道	１ (1) −32　　(2) 25−3＝22 　　(3) 4√5＋2√5＝6√5 ２ 与式＝72＋2×7×(−3)＝49−42＝7 ３ x軸の式はy＝0だから, 　　　これを代入して,0＝−2x＋8 　　　2x＝8で,x＝4　　よって, A(4,0) ４ 連立方程式の形を2つに分ける 3x−2y＝5 …ア −x＋4y＝5 …イ 　ア×2＋イより,5x＝15で,x＝3 　これをイに代入して,−3＋4y＝5 　　4y＝5＋3で,y＝2 　よって, x＝3,y＝2 ５ x≦10 ６ 中点連結定理より,AE＝ECとなるから, 　　ECの中点をPとすればよい。 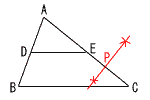・2点EとCから等距離の 　点を2つとる ・2つの点を結んで,ECの 　垂直二等分線をひく ・垂直二等分線とECの 　交点をPとする	４岩手県	１ 1＋3＝4 ２ 15x÷5＋20÷5＝3x＋4 ３ 　　5×√2 . ＝ 5√2 　√2×√2 2 ４ (x−7)(x＋2) ５ 解の公式より, 　x＝ −(−7)±√(−7)2−4×1×11 2×1 　　＝ 7±√49−44 ＝ 7±√5 2 2 　〜２番問題 （おまけ）〜 1000−3x＝y　　(3x＋y＝1000なども可) 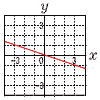　〜３番問題 （おまけ）〜 右図のグラフ 　原点を通り,傾き−の直線
２青森県	１ ア 2 　イ − 4 × 3 ＝− 12 ＝− 3 　(−0.12も可) 10 10 100 25 　ウ 　1−6 x＋ 2＋1 y＝− x＋ y 　3 2 　　　 ( −10x＋9y も可） 6 　エ 　　　　24ab2　　. ＝ 24ab2 ＝2b 　(−6a)×(−2b) 12ab 　オ (√5−√2)(√5＋√2)＝5−2＝3 ２ 92π× 60 ＝81π× ＝ 27 πcm2 360 2 ３ 2乗して比較すると, 　順に, 7.29, 49/9(5.4), 9, 6 だから, 　　最大は−3 ４ 26x＋8y＝380 …ア 1.5x＋4y＝75 …イ 　ア−イ×2より,23x＝230で,x＝10 　これをイに代入して,4y＝75−15で,y＝15 　よって, ドーナツ10個,クッキー15個 ５ 最大値は0だから,グラフは上に凸 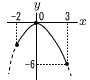(右図参照) y＝ax2に(3,-6)を代入して, 　−6＝9aより, a＝− ６ △OABは二等辺三角形 　∠OAB＝∠OBA＝20° 　∠BAC(円周角)＝96÷2＝48° 　20＋x＝48より, ∠x＝28° ７ 回数データを順に並べ替えると, 　　2,3,4,5,5,6,7,8,9,9,10 4等分したときの境目の数は,3・6・9番目 　よって, 9−4＝5回	５山形県	１ (1) −7＋2−1＝−6 　(2) 　−3×5 ＋ 1 ＝− 5 ＋ 4 ＝− 　4×6 2 8 8 　 　(3) 　−6xy2 ＋ 　8xy . ＝3y−4 　−2xy −2xy ２ 3x2−5x−2＝x−1 　3x2−6x−1＝0 解の公式より, 　x＝ −(−3)±√(−3)2−3×(−1) 3 　　＝ 3±√9＋3 ＝ 3±2√3 3 3 ３ 5枚から2枚の取り出し方は全部で, 　5×4÷2＝10通り 余り1になるのは,次の4通り 　(大,小)＝(3,2) (4,3) (5,2) (5,4) よって, 確率＝ 4 ＝ 10 ４ エ ５ ア
３秋田県	【前期】 １ 7＋6＝13　　２ 5a＋b (g) ３ 3√2− 8×√2 ＝3√2−4√2＝−√2 √2√2 ４ x(y−1)＋5(y−1)＝(x＋5)(y−1) ５ 連立方程式の形を,2つに分ける x＋2y＝1 …ア 4x＋7y＝1 …イ 　ア×4−イより,y＝3 　これをアに代入して,x＋6＝1で,x＝−5 　よって,x＝−5,y＝3 ６ 解の公式より, 　x＝ −7±√72−4×2×(−4) ＝ −7±√81 2×2 4 　　＝ −7±9 ＝ ,−4 4 [別解] 　因数分解すると, (2x−1)(x＋4)＝0 　　よって, x＝,−4 ７ a(傾き)＞0だから,右上がり 　 b(切片)＜0だから,y軸と負で交わる 　よって, イ 　〜２番問題 （おまけ）〜 １ ア 22＋(2√3)2＝42 　 ウ 0.62＋0.82＝12 　　よって, ア,ウ ２ 6枚から2枚の取り出し方は全部で, 　6×5÷2＝15通り 和が7以上になるのは,次の9通り 　(1,6) (2,5) (3,4) (2,6) (3,5) (3,6) (4,5) 　(4,6) (5,6) 　 よって, 確率＝ 9 ＝ 15 ３ 19.1mは15〜20mの階級で,度数は8人 　よって, 相対度数＝8÷25＝0.32 ４ x:9＝6:(6＋2) 　8x＝54より, x＝ 54 ＝ 27 8 4 【一般】 １ −3×(−3)＝9 ２ 　a2×ab2 ＝ a3b2 ＝b2 　a3b a3b ３ 4√5×√5＝4×5＝20 ４ √2, π ５ 上式＋下式×4より,3x＝21で,x＝7 　これを上式に代入して,7＋y＝9で,y＝2 　よって, x＝7,y＝2 ６ (x＋1)(x＋2)＝0より, x＝−1,−2 ７ y＝に(2,4)を代入して, 　4＝ a で,a＝8　　よって, y＝ 8 2 x ８ 白石をx個とすると,比率より, x ＝ 18 で,x＝18×500÷60＝150 500 60 　よって, およそ150個 ９ 与式＝(5x＋y)(5x−y)＝(55＋54)(55−54) 　　＝109×1＝109 10 148−4＝144, 245−5＝240 144と240の公約数のうち,6以上は, 　最大公約数が48だから,6,8,12,16,24,48 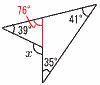　よって, 6個 11 x:15＝12:18＝2:3 　3x＝30より, x＝10 12 (右図参照) 　41＋35＝76° 　∠x＝76＋39＝115° 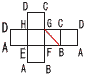13 右図 (記号は不要) 14 扇形(側面)の弧は6πcm, 母線をaとすると, 　×6π×a＝24πで,a＝8 円錐の高さ＝√82−32＝√55 よって, 体積＝×32π×√55＝3√55πcm3 15 全体−(周りの4立体) 三角錐A-BDM＝(×62)×6＝36 三角錐B-CDG＝(×62)×12＝72 四角錐G-BMEF＝四角錐G-DMEH 　＝×(6＋12)×6×6＝108 よって,62×12−(36＋72＋108×2)＝108cm3	６宮城県	１ −11 ２ 6＋4＝10 ３ 　3xy2 ＝ y 　( yも可) 　15xy 5 ４ 与式＝−a＋5b＝−(−1)＋5×＝1＋3＝4 ５ √18−√2＝3√2−√2＝2√2 ６ (x−4)(x＋3)＝0より, x＝4,−3 ７ y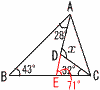＝に(−5,2)を代入して, 　2＝ 　a . より,a＝−10 −5 　y＝− 10 に,x＝3を代入して, y＝− 10 x 3 ８ (右図参照) ∠AEC＝28＋43＝71° ∠x＝71＋32＝103° [別解]へこんだ四角形では, 　∠x＝28＋43＋32＝103°
		７福島県	１ −6 ２ −14 ３ 5a−10b−4a＋6b＝a−4b ４ 2√3×3√5＝6√15 ５ 52π× 72 ＝25π× ＝5πcm2 360 　〜２番問題 （おまけ）〜 １ 16a＋b≧250 ２ 傾き2で右上がり,切片は−3で, ウ ３ (x−2)2＝6 　　x−2＝±√6 　　x＝2＋√6 ４ データを順に並べ替えると, 　　　4,7,9,10,11,13,18,18,20,25 中央値＝(11＋13)÷2＝12分 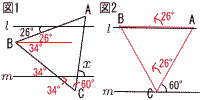５ (右図参照) 図1より, ∠x＝180−(34＋60) 　＝180−94＝86° [別解] 図2より,△ABCを26° 　回転させると考えて, ∠x＝60＋26＝86°
		８茨城県	１ (1) 4＋9−13 　　(2) √18−√8＝3√2−2√2＝√2 　　(3) 　6a3×b ＝a2b2 　3×2a 　(4) 　2(x＋6y)＋3(3x−4y) 　3×2 　　　＝ 2x＋12y＋9x−12y ＝ 11 6 6 ２ x2−4x−21＋21＝0 　　x(x−4)＝0より, x＝0,4 　〜２番問題 （おまけ）〜 １ 与式に(−6,1)を代入すると, −6a＋b＝−11 …ア −a−6b＝−8 …イ ア×6＋イより,−37a＝−74で,a＝2 これをイに代入して,−2−6b＝−8で,b＝1 　よって, a＝2,b＝1 ２ 数の出方は全部で,6×6＝36通り 点がグラフ上にあるのは,次の4通り 　(a,b)＝(-3,-2) (-2,-3) (2,3) (3,2) よって, 確率＝ 4 ＝ 36 ３ 1着の定価をx円とすると, 　2x＋0.7x×3＝8200 　　4.1x＝8200 　　x＝8200÷4.1＝2000円