| 1 |
(1) |
 2-5 2-5
|
5 |
| 回数(回) |
人数(人) |
| 0 |
1 |
| 1 |
4 |
| 2 |
[ア] |
| 3 |
[イ] |
| 4 |
2 |
| 計 |
12 |
 A中学校バスケットボール部の1年生12人が,シュート練習を4回ずつ行った。右の表はシュートが成功した回数と人数の関係をまとめたものである。12人について,シュートが成功した回数の中央値が2回であるとき,[ア],[イ]にあてはまる数の組み合せは全部で何通りあるか,求めなさい。 A中学校バスケットボール部の1年生12人が,シュート練習を4回ずつ行った。右の表はシュートが成功した回数と人数の関係をまとめたものである。12人について,シュートが成功した回数の中央値が2回であるとき,[ア],[イ]にあてはまる数の組み合せは全部で何通りあるか,求めなさい。
|
| (2) |
 9÷(-3)-42 9÷(-3)-42
|
| (3) |
| 6a2b3÷ |
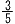 |
ab2 |
|
| (4) |
|
2番問題 ~ おまけ ~
100円と50円の硬貨がある。 |
| (5) |
|
1 |
100円と50円の硬貨を合わせて320枚入れた袋がある。よくかき混ぜてから,ひとつかみ取り出して100円と50円の硬貨の枚数を調べたところ,100円硬貨は27枚,50円硬貨は21枚あった。
このとき,袋の中に入っていた100円硬貨はおよそ何枚と考えられるか,求めなさい。
|
| 2 |
次の方程式を解きなさい。
2x2-5x-1=0
|
| 3 |
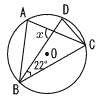 右の図のように,円Oの周上に4点A,B,C,Dがあり,点Cを含まない 右の図のように,円Oの周上に4点A,B,C,Dがあり,点Cを含まない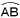 の長さが,点Aを含まない の長さが,点Aを含まない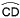 の長さの2倍である。このとき,∠xの大きさを求めなさい。 の長さの2倍である。このとき,∠xの大きさを求めなさい。
|
2 |
 100円硬貨が1枚,50円硬貨が2枚ある。この3枚を同時に投げたとき,表が出た硬貨の合計金額をa円,裏が出た硬貨の合計金額をb円とする。 100円硬貨が1枚,50円硬貨が2枚ある。この3枚を同時に投げたとき,表が出た硬貨の合計金額をa円,裏が出た硬貨の合計金額をb円とする。
このとき, a-b≧100 が成り立つ確率を求めなさい。
また,その考え方を説明しなさい。説明においては,図や表,式などを用いてよい。ただし,硬貨の表裏の出かたは同様に確からしいとする。
|
| 4 |
関数 y=x2 について,xの値がaからa+3まで増加するときの変化の割合が13である。このときのaの値を求めなさい。
|
 右の図のように,円Oの周上に4点A,B,C,Dがあり,点Cを含まない
右の図のように,円Oの周上に4点A,B,C,Dがあり,点Cを含まない