全国公立高校入試 　１番問題　【令和３年春】	正　答　６
	41　佐賀県　〜　47　沖縄県

41佐賀県	１ (1) 5＋7＝12 　　(2) −8×＝−6 　　(3) x＋3y−2x＋2y＝−x＋5y 　 (4) 2−2√2＋1＝3−2√2 ２ (x−5)(x＋7) ３ 解の公式より, 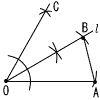　x＝ −5±√52−4×1×1 2×1 　＝ −5±√25−4 ＝ −5±√21 2 2 ４ 81π:G＝33:53 　27G＝81π×125 　G＝3π×125＝375πcm3 ５ 右図 ・OA＝OC＝ACとなる点Cをとる 　　(∠AOC＝60°) ・∠AOCの二等分線lをひく ・l上にOA＝OBとなる点Bをとる 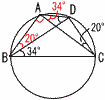６ (右図参照) 　∠BAC＝90°(BCは直径) 　∠ABD＝20° 　∠CAD＝34° △ABDで 　∠ADB＝180−(34＋90＋20) 　　＝180−144＝36° ７ �@ E　　�A 75分 誤りの表について 　5人の合計は,73×5−362＝3分足りない 　中央値は, 68,70,72,74,78になっている 　よって,Eを72分→75分にすればよい	44熊本県	１ 　7＋6 ＝ 13 　　２ 8−28＝−20 　21 21 ３ 3x＋3y−2x＋12y＝x＋15y ４ 　36a2×2ab2 ＝−8ab 　−9a2b ５ 4x2＋4x＋1＋5x2−4x−1＝9x2 ６ 　5√2 ＋ 　3　. ＝ 5√2＋3√2 ＝2√2 　4 2√2 4 　〜２番問題の一部 （おまけ）〜 １移項して3x＝−6より, x＝−2 ２ 移項して, x2−x−9＝0 解の公式より, 　x＝ −(−1)±√(−1)2−4×1×(−9) 2×1 　＝ 1±√1＋36 ＝ 1±√37 2 2 ３ 　変化の割合＝ a×42−a×12 ＝ 16a−a ＝4 4−1 3 　15a＝4×3より, a＝ 12 ＝ 15 [放物線の変化の割合] 放物線y＝ax2で,xがp→qに変化するとき, 　変化の割合＝ aq2−ap2 ＝ a(q＋p)(q−p) q−p q−p 　　＝a(p＋q) 上記の３では, 　変化の割合＝a(p＋q)＝a(1＋4)＝4で, 　　5a＝4が簡単に求められる。
42長崎県	１ 8÷（−2)＝−4 ２ 3√5− 10√5 ＝3√5−2√5＝ √5 √5√5 ３ y＝に(4,8)を代入して, 　8＝a/4で, 比例定数a＝32 　y＝32/xに,x＝2を代入して, 　　y＝32/2＝16 ４ 4x−y＝30 　(4x＝30＋y等も可) ５ 上式×2＋下式より 　5x＝15で,x＝3 　これを上式に代入して 　　3＋2y＝−1で,y＝−2 　よって, x＝3, y＝−2 ６ (x−2)2＝5より,x−2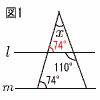＝±√5 　よって, x＝2±√5 ７ (右図参照) 　l の上側の三角形で, 　　同位角74°を考える 　∠x＝110−74＝36° ８ 順に5000,4100,4010,4001,3200,… 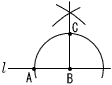　よって5番目は, 3200 ９ 右図 ・Bからl に垂線をひく ・垂線上に, 　　BA＝BCとなる点Cをとる 10 右下図 　斜辺が√10の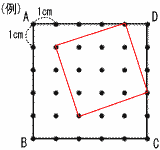直角 　　三角形を作る	45宮崎県	１ −9　　　２ 　　　３ 1−9＝−8 ４ −4a＋4b＋5a−10b＝a−6b ５ √4＋√9＝2＋3＝5 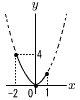６ 移項して, x2−10x＋21＝0 　(x−3)(x−7)＝0より, x＝3,7 ７ (右図参照) 　x＝−2のとき,y＝(−2)2＝4 　よって, 0≦y≦4 ８ イ,ウ 　イ…平均値が小さいから,合計も小さい 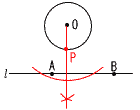　ウ…範囲はともに15m ９ 右図 ・円Oと直線ｌとの距離が 　最短であればよいから, 　　垂線をおろす ・垂線と円周の交点に点Pをとる
		46鹿児島県	１ (1) 20＋7＝27 　(2) 　2 − 3×2 ＝ 10 − 2 ＝ 8 　3 5×9 15 15 15 　(3) √48− 9√3 ＝4√3−3√3＝√3 √3√3 　(4) 20分で4kmだから,60分で4×3＝12km 　　　時速12km 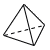　(5) (右図参照)　6本 ２ x＝5を代入すると, 　35−3a＝20＋2a 　−5a＝−15で, a＝3 ３ 三平方の定理より, 　高さ＝√52−32＝4cm 　体積＝×3×4×7＝42cm3 ４ 28＝22×7より, n＝7 ５ ウ 　1193÷813≒1.467
43大分県	１　(1) 5 　　(2) 5−9×2＝5−18＝−13 　　(3) 3a−6b−4a−2b＝−a−8b 　　(4) 　5(x＋2y)＋3(x−y) 　15 　　　　＝ 5x＋10y＋3x−3y ＝ 8x＋7y 15 15 　　(5) 3√2− 　4√2 . ＝3√2−2√2 √2√2 　　　　　＝√2 ２ 解の公式より, 　x＝ −(−3）±√（−3)2−4×1×(−2) 2×1 　＝ 3±√9＋8 ＝ 3±√17 2 2 ３ 与式にx＝2を代入して, 　6＋2a＝5−2a 　移行して,4a＝−1 　a＝− ４ 積が9の倍数になるのは次の4通り 　(大,小)＝(3,3),(3,6),(6,3),(6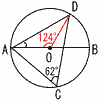,6) 　確率＝4/36＝ ５ (右図参照) 　△OADで 　　∠AOD＝62×2＝124° 　△OADは二等辺三角形 　∠BAD＝(180-124)÷2＝28° 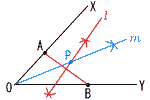６ 右図 ・線分ABの垂直 　　二等分線lを引く ・∠XOYの二等分 　　線mを引く ・lとmの交点に 　　点Pをとる	47沖縄県	１ 2−9＝−7 ２ −14 ３ 6＋2＝8 ４ 4√3＋2√3＝6√3 ５ 　6ab2×3a ＝18a2b 　b ６ 3x−y＋2x＋2y＝5x＋y 　〜２番問題の一部 （おまけ）〜 1 4x−x＝−6−3 　3x＝−9より, x＝−3 ２ 下式×2−上式より 　7y＝14で, y＝2 　これを下式に代入して, 　　x＋4＝8で, x＝4 　よって, x＝4, y＝2 ３ x2−6x＋9 ４ (x＋4)(x−2) ５ 解の公式より, 　x＝ −3±√32−4×2×(−1) 2×2 　＝ −3±√9＋8 ＝ −3±√17 2 2 ６ 32π× 60 ＝9π× ＝ π 360

［トップに戻る］　［前ページに戻る］