|
正 答 4 | |||
| 25 滋賀県 〜 32 島根県 |
|
正 答 4 | |||
| 25 滋賀県 〜 32 島根県 |
| 25滋賀県 | 1 −6+1=−5
7y=−7で, y=−1 これを下式に代入して, 2x−1=5で, x=3 よって, x=3, y=−1
(x+3)(x−2)=0より, x=−3,2
6=42aで,a=6/16= y= b= 8 できる素数は次の8通り 11,13,23,31,41,43,53,61 確率=8÷36= 9 (ア) アをxとすると,総時間より, 5×5+15×10+25x+35×4 =(5+10+x+4)×20 25+150+25x+140=20(x+19) 25x−20x=380−315 5x=65で, x=13 (イ) 5+10+13+4=32 最頻値は13人で, 25分 |
28兵庫県 | 1 −7+2=−5 2 −3x 3 4√5−2√5=2√5 4 (x+2y)(x−2y) 5 解の公式より,
6 S=4πr2=4π×22=16π cm2 7 (右図参照) 110°を平行線で分割 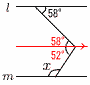 ∠x=180−52=128° ∠x=180−52=128°8 中央値は13番目の, 400〜500gの階級で,3人 よって, 3÷25=0.12 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26京都府 | 【 前期 】 1 4+36×
4 y= y=−24/xにx=4を代入して, y=−24/4=−6 5 次の連立方程式を解く
これをアに代入して, 2x−3=15より, x=9 よって, x=9, y=−1 6 1つの外角をx°とすると, 内角+外角=180°より, 9x+x=10x=360で, x=36 外角の和は180だから, 180÷36=20本 7 √9<√10<√16より,3<√10<4 よって,-3,-2,-1,0,1,2,3の 7個 8 解の公式より,
9 イ n=16 ・順に並び替えると, 11,12,14,15,21 中央値が15より, 誤りは11,12,14のいずれか ・合計は平均値15×5より, 誤りは2本不足 ・11,12,14に2を加えて15より大きくなる のは,火曜日の14本 |
29奈良県 | 1 (1) −7 (2) −9×9=−81
2 上式+下式×4より 11x=−11で,x=−1 これを下式に代入して,−2−y=−3 −y=−3+2で,y=1 よって, x=−1, y=1 3 解の公式より,
√15の整数部分は3で, a=√15−3 与式=a(a+6)=(√15−3)(√15−3+6) =(√15−3)(√15+3)=15−9=6
6 (右図参照) ウ 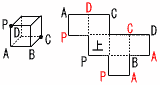 7 右下図 ・ABを1辺とする正三角 形をかく 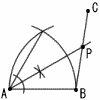 ・∠Aの二等分線うをひく ・∠Aの二等分線うをひく・BCとの交点をPとする 8 (1) a+3 (2) 2021÷3=673余り2 3数の和は,3a+(3〜6)の4通り このうち余りが2になるのは3a+5 つまり,a+1を除く 3a+5=2021より,a=672 よって,a+1=672+1=673 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 【 中期 】 1 16+3=19
x=−1±6√2
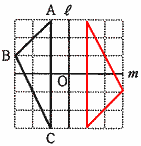 7 右図 7 右図8
4通り ・4枚とも表は1通り |
30和歌山県 | 1 (1) −4
2 解の公式より,
3 移項して, 3y=8−4x
4 13.5≦a<14.5 5 中央値は5・6番目の平均値で (20+22)÷2=21m 最頻値は最多3人の, 17m |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27大阪府 | 【 A 】 1 10−16=−6
3 25−21=4 4 6x−3−4x−4=2x−7 5 −5x3 6 √7+2√7=3√7 〜2番問題(おまけ)〜 1 −(−3)+8=3+8=11 2 ウ 時間=道のり÷速さ=a/70 3 イ (エ √9=3) 4 2x=12×3より, x=18 5 上式+下式より, 8x=8で,x=1 これを上式に代入して, 5+2y=−5で,y=−5 よって, x=1, y=−5 6 (x+3)(x−7)=0で, x=−3, 7 |
31鳥取県 | 1 (1) −2 (2)
3 与式=(−3)2+4×(−3)=9−12=−3 4 (x+6)(x−1) 5 両辺×6より,3(5−3x)−(x−1)=6 −9x−x=6−15−1 −10x=−10で, x=1 6 解の公式より,
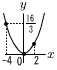 8 (右図参照) 8 (右図参照)(1) y=ax2に(6,12)を代入して, 12=36aで, a= (2) x=−4のとき,y= よって, 0≦y≦
積abが12以上は 17通りだから,
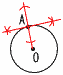 10 右図 10 右図点AからOAの垂線を引けばよい |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 【 B 】 1 2×9−22=18−22=−4 2 4x−4y+10x+5y=14x+y
5 4−4√5+5=9−4√5 6 七角形の内角の和=三角形5個分 180×5=900° 7 エ たとえば,a=1,b=−1と考えてみる 8 26〜28回で4人だから,4÷12=0.33 9 取り出し方は,5×4÷2=10通り 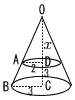 a=3×6,5×6,6×7の3通り a=3×6,5×6,6×7の3通りよって, 確率=3÷10= 10 (右図参照) △OAD∽△OBCより x:(x+3)=2:3 3x=2x+6で,x=6 円錐台=大円錐−小円錐
|
32島根県 | 1 4−6=−2 2 (x+6)(x+2)=0より, x=−6,−2 3 上式+下式×2より, 7x=14で,x=2 これを下式に代入して, 4+y=7で,y=3 よって, x=2, y=3 4 3a+5b=1685
√3≒1.7 7 y= 2=a/(−4)で,比例定数a=−8 よって式は, y= 8 △EAF(二等辺三角形)で, 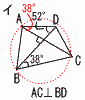 ∠EAF=(180−30)÷2=75° ∠EAF=(180−30)÷2=75°∠BAF=∠C=130° よって, ∠x=130−75=55° 9 (右図参照) イ ∠CAD=90−50=38°=∠CBD 10 (0,0) (0,50) (50,0) の3通り よって, 確率=3÷9= |
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] |