| 1 |
(1) |
 3+(-5) 3+(-5)
|
7 |
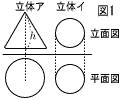 右の図1は2つの立体の投影図である。立体アと立体イは,立方体,円柱,三角柱,円錐,三角錐,球のいずれかであり,2つの立体の体積は等しい。 右の図1は2つの立体の投影図である。立体アと立体イは,立方体,円柱,三角柱,円錐,三角錐,球のいずれかであり,2つの立体の体積は等しい。
平面図の円の半径が,立体アが4cm,立体イが3cmとき,立体アの高さhの値を求めなさい。
|
| (2) |
|
| (3) |
|
8 |
関数 y=ax2 のグラフが点(6,12)を通っている。
(1) aの値を求めなさい。
(2) xの変域が-4≦x≦2のとき,yの変域を求めなさい。
|
| (4) |
3(x+y)-2(-x+2y)
|
| (5) |
-4ab2÷(-8a2b)×3a2
|
| 2 |
(3x-y)2
|
9 |
 右の図2のような1~6までの目がある1個のさいころを2回投げて,1回目に出た目をa,2回目に出た目をbとする。このとき,積abの値が12未満となる場合と12以上となる場合とでは,どちらの方が起こりやすいか,次のア~ウからひとつ選び,記号で答えなさい。また,そのように判断した理由を,確率を計算し,その値を用いて説明しなさい。 右の図2のような1~6までの目がある1個のさいころを2回投げて,1回目に出た目をa,2回目に出た目をbとする。このとき,積abの値が12未満となる場合と12以上となる場合とでは,どちらの方が起こりやすいか,次のア~ウからひとつ選び,記号で答えなさい。また,そのように判断した理由を,確率を計算し,その値を用いて説明しなさい。
ただし,さいころの目はどの目が出ることも同様に確からしいものとする。
| ア |
12未満になることの方が起こりやすい。 |
| イ |
12以上になることの方が起こりやすい。 |
| ウ |
どちらも起こりやすさは同じ。 |
|
| 3 |
a=-3のとき, a2+4a の値を求めなさい。
|
| 4 |
x2+5x-6=0 を因数分解しなさい。
|
| 5 |
| 一次方程式 |
5-3x |
- |
x-1 |
=1 を解きなさい。 |
| 2 |
6 |
|
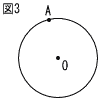
10 |
次の図3の円Oで,点Aが接点となるように,円Oの接線を作図しなさい。ただし,作図に用いた線は明確にして,消さずに残しておくこと。
|
| 6 |
二次方程式 x2-x-1=0 を解きなさい。
|
 |
 右の図1は2つの立体の投影図である。立体アと立体イは,立方体,円柱,三角柱,円錐,三角錐,球のいずれかであり,2つの立体の体積は等しい。
右の図1は2つの立体の投影図である。立体アと立体イは,立方体,円柱,三角柱,円錐,三角錐,球のいずれかであり,2つの立体の体積は等しい。 右の図2のような1~6までの目がある1個のさいころを2回投げて,1回目に出た目をa,2回目に出た目をbとする。このとき,積abの値が12未満となる場合と12以上となる場合とでは,どちらの方が起こりやすいか,次のア~ウからひとつ選び,記号で答えなさい。また,そのように判断した理由を,確率を計算し,その値を用いて説明しなさい。
右の図2のような1~6までの目がある1個のさいころを2回投げて,1回目に出た目をa,2回目に出た目をbとする。このとき,積abの値が12未満となる場合と12以上となる場合とでは,どちらの方が起こりやすいか,次のア~ウからひとつ選び,記号で答えなさい。また,そのように判断した理由を,確率を計算し,その値を用いて説明しなさい。