全国公立高校入試 　１番問題　【令和３年春】

（２９）奈良県

学習日　　　 月　　 　日（　　　）

印刷して、紙の上でやってネ！ 　印刷用

１	(1)	－2－5	５	階級 (時間) 度数(人) A中 B中 以上 未満 4 ～ 5 1 7 5 ～ 6 5 5 6 ～ 7 7 25 7 ～ 8 12 31 8 ～ 9 4 3 9 ～ 10 1 2 計 30 73 　右の表は,A中学校とB中学校の3年生全生徒を対象に,1日当たりの睡眠時間を調査し,その結果を度数分布表にまとめたものである。この表から読み取ることができることがらとして適切なものを,次のア～工からすべて選び,その記号を書け。 ア 5時間以上6時間未満の階級の相対 　度数は,A中学校の方が大きい。 イ 睡眠時聞が8時間以上の生徒の人数は,A中学校の方が 　多い。 ウ 睡眠時間の最頻値(モード)は,B中学校の方が大きい。 工 B中学校の半数以上の生徒が,7時間未満の睡眠時間で 　ある。
	(2)	－32×9
	(3)	8a2b÷(－2ab)2×6ab
	(4)	(x＋7)(x－4)－(x－4)2
２	連立方程式 3x＋4y＝1 を解け。 2x－y＝－3		６	図1は,立方体の展開図である。この展開図を組み立てて図1できる立体において,頂点Pと頂点A,B,C,Dをそれぞれ結ぶ線分のうち,最も長いものはど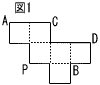れか。次のア～工から1つ選び,その記号を書け。 　ア 線分PA　　イ 線分PB 　ウ 線分PC　　工 線分PD
３	2次方程式 x2－3x＋1＝0 を解け。		７	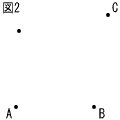図2のように,3点A,B,Cがある。次の条件①,②を満たす点Pを,定規とコンパスを使って解答欄の枠内に作図せよ。なお,作図に使った線は消さずに残しておくこと。 [条件] 　① 点Pは,線分BC上にある。 　② ∠BAP= 30°である。
４	√15の小数部分をaとするとき,a2＋6aの値を求めよ。		８	連続する4つの整数のうち,1つの数を除いた3つの整数の和は2021である。 (1) 連続する4つの整数のうち,最も小さい数をaとするとき,最も大きい数をaを用いて表せ。 (2) 除いた数を求めよ。