全国公立高校入試 　１番問題　【令和３年春】

（８）茨城県

学習日　　　 月　　 　日（　　　）

印刷して、紙の上でやってネ！ 　印刷用

１　番　問　題		２番問題　～おまけ～
１	A,B,C,Dの4つのチームが自分のチーム以外のすべてのチームと試合を行った。下の表は.その結果をまとめたものである。得失点差とは,得点合計から失点合計をひいた値である。 　このとき.下の[ア]に当てはまる数を求めなさい。 チーム 試合数 勝った 試合数 引き分けた 試合数 負けた 試合数 得点 合計 失点 合計 得失 点差 A 3 2 1 0 8 1 +7 B 3 1 1 1 3 7 ア C 3 1 1 1 4 4 0 D 3 0 1 2 1 4 -3	１	｢連続する3つの整数の和は. 3の倍数である｣ このことを次のように説明した。 (説明) 　連続する3つの整数のうち,もっとも小さい整数をnとすると,連続する3つの整数は小さい順にn,[ア],[イ] と表すことができる。 　ここで, n＋([ア])＋([イ])＝3([ウ]) [ウ]は整数だから,3([ウ])は3の倍数である。 したがって,連続する3つの整数の和は3の倍数である。 　このとき上の[ア]～[ウ]に当てはまる式を,それぞれ書きなさい。
２	下の図のように,長方形ABCDの中に1辺の長さが√5mと√10mの正方形がある。 　このとき,斜線部分の長方形の周の長さを求めなさい。	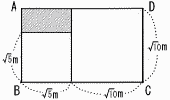２	太郎さんは庭に,次の2つの条件①,②を満たすような長方形の花だんを作ることにした。 (条件) 　① 横の長さは,縦の長さより5m長い。 　② 花だんの面積は,24m2である。 　縦の長さをxmとして方程式をつくると,次のようになる。 　　[ア]＝24 　したがって,この方程式を解くと,x＝[ア],[イ]となる。 　x＝[イ]は,縦の長さとしては適していないから,縦の長さは[ウ]mである。 　このとき上の[ア]には当てはまる式を,[イ],[ウ]には当てはまる数をそれぞれ書きなさい。
３	1000円で,1個a円のクリームパン5個と1個b円のジｬムパン3個を買うことができる。ただし,消費税は考えないものとする。 　この数量の関係を表した不等式としてもっとも適切なものを,次のア～工の中から一つ選んで,その記号を書きなさい。 　ア　1000－(5a＋3b)＜0　 イ　5a＋3b＜1000 　ウ　1000－(5a＋3b)≧0　 工　5a＋3b≧1000	３	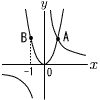下の図で,点Aは関数y＝ と関数y＝ax2の グラフの交点である。点Bは点Aをy軸を対称の軸として対称移動させたものであり,x座標は－1である。 　このことから,aの値は[ア]であり，関数y＝ax2について,xの値が1から3まで増加するときの変化の割合は[イ]であることがわかる。 　上の[ア],[イ]に当てはまる数をそれぞれ書きなさい。
４	花子さんは,下の図の平行四辺形ABCDの面積を求めるために,辺BCを底辺とみて,高さを測ろうと考えた。 　点Pを下の図のようにとるとき,線分PHが高さとなるような点Hを作図によって求めなさい。 　ただし,作図に用いた線は消さずに残しておくこと。	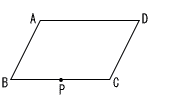４	陸上競技部のAさんとBさんは100m競走の選手である。下の図は,2人が最近1週間の練習でそれぞれ100mを18回走った記録をヒストグラムに表したものである。これらのヒストグラムをもとに,次の1回でより速く走れそうな選手を1人選ぶとする。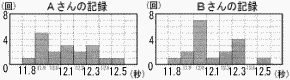 　このとき,あなたならどちらの選手を選びますか。Aさん,Bさんのどちらか一方を選び,その理由を,2人の中央値(メジアン)または最頻値(モード)を比較して説明しなさい。