全国公立高校入試 　１番問題　【令和２年春】	正　答　３
	17　石川県　〜　24　三重県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

17石川県	１ (1) −9 　 (2) 7−32＝−25 　(3) 　9a2×5 ＝b 　6a2b 　(4) 　3(x＋3y)−4(2x−y) 　4×3 　　＝ 3x＋9y−8x＋4y ＝ 　−5x+13y 12 　12 　(5) √20−√45＝2√5−3√5＝−√5 ２ 解の公式より, 　x＝ −5±√52−4×1×(−3) 2×1 　　＝ −5±√25＋12 ＝ −5±√37 2 2 ３ a−5b≧20 ４ x＋y＝2√7,x−y＝2√2より, 与式＝(x＋y)(x−y)＝2√7×2√2 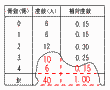　＝4√14 ５（右図参照） 6人の相対度数が0.15だから, 　計は,6÷0.15＝40人 平均値は, 　(0×6＋1×6＋2×12＋3×10 　　　＋4×6)÷40 　＝(0＋6＋24＋30＋24)÷40 　＝84÷40＝2.1冊	22静岡県	１ (1) 5−24＝−19　　(2) 5a−2b 　(3)　  7(x−y)−2(x＋3y) ＝ 5x−13y  2×7 14 　(4) 6√7＋3√7＝9√7 ２ 与式＝9a2＋24a＋16−9a2−18a＝6a＋16 　＝6×＋16＝7＋16＝23 ３ x2−4x−21＝0 　(x−7)(x＋3)＝0より,x＝7,−3 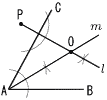　〜２番問題（おまけ）〜 １ 右図 ・PからACの垂線l を引く ・∠Aの二等分線mを引く ・l とmの交点をOとする 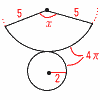２（右図参照） 底面の円周は4πcmだから、 　10π×＝4πより, 　x＝4π÷10π×360＝144° ３ 引き方は全部で, 　　　6×5÷2＝15通り 　公約数が1しかないのは, 　 1と2，1と3，1と4，1と5，1と6，2と3， 　2と5，3と4，3と5，4と5，5と6 の11通り 　よって,確率＝11÷15＝
18福井県	１ (1) 3−2×9＝3−18＝−15 　 (2) 2√3− 　6√3 . ＝2√3−2√3＝0 √3√3 　(3) 2b×2b＝4b2 ２ (a−6)(a＋1) ３ 2x2＋5x＋2＝2x＋3 　2x2＋3x−1＝0 解の公式より, 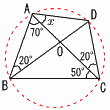　x＝ −3±√(32−4×2×(−1) 2×2 　　＝ 1−3±√9＋8 ＝ −3±√17 4 4 ４ ア,ウ ５（右図参照） ∠ABD＝∠ACD＝70° 　ABCDは円に内接する (x＋70)＋(50＋20)＝180 　∠x＝180−140＝40° ６ 右下図 ∠APB(円周角)＝30° ∠AOB(中心角)＝60° 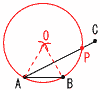　　なる円をかけばよい ・線分ABを1辺とする 　　正三角形OABを作図 ・円OとACの交点をPとする 　〜２番問題（おまけ）〜 １ 変化の割合＝ 42−12 ＝ 15 ＝5 4−1 3 ２ 0＜＜3だから, ア	23愛知県	【　Ａ　】 １ 3＋8＝11 ２   10(2x−3)−3(3x−10) ＝ 11 x  3×5 15 ３ √5(√2＋1)･√3(√2−1)＝√15(2−1)＝√15 ４ 展開して整理すると,x2−x−3＝0 解の公式より, 　x＝ −(−1)±√(−1)2−4×1×(−3) 2×1 　　＝ 1±√1＋12 ＝ 1±√13 2 2 ５ 与式＝(5x2−10x)−(4x2−9) 　　　＝x2−10x＋9＝(x−1)(x−9) ６ クラスの人数をx人とすると, 　300x＋2600＝400x−1200 　−100x＝−3800より,x＝38人 ７ 2秒後,4秒後の距離を求めると, 　x＝2のとき,y＝3×22＝12m 　x＝4のとき,y＝3×42＝48m 平均速度＝ 48−12 ＝18m/分 4−2 ８ 積が奇数になるのは,奇数×奇数の場合で, 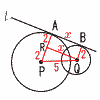　確率＝×＝ ９（右図参照） 　AB＝xとすると,△PQRで, 　　x2＝22＋52より,x＝√21cm
19山梨県	１ 10＋4＝14 ２ − 7×31 ＋ 4 ＝ −7＋4 ＝− 3 155 5 5 5 ３ 9＋7＝16 ４ 2√6＋8√6＝10√6 ５ 　27xy×x2 ＝−3x 　−9x2y ６ 3x＋18y−2x−16y＝x＋2y 　〜２番問題（おまけ）〜 １ 解の公式より, 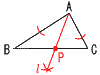　x＝ −(−7)±√(−7)2−4×2×4 2×2 　　＝ 7±√49−32 ＝ 7±√17 4 4 ２ 右図 ・∠Aの二等分線l を引く ・l とBCの交点をPとする ３ y＝axに(−3,36)を代入して, 　36＝−3aで,a＝−12 　よって,y＝−12x		【　Ｂ　】 １ 4＋3＝7 ２ (6x2＋x−1)−(6x2−x−1)＝2x ３ 5−2√5＋1＋2√5＝6 ４ 展開して整理すると,x2−3x−4＝0 　(x−4)(x＋1)−0より,x＝4,−1 ５ 5a＋b＜500 ６ Aがx人,Bがy人とすると, 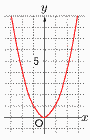　{ x:y＝1:2 …ア (x＋14):(y−14)＝5:7 …イ アより,y＝2x…ウ で,これをイに代入すると、 　7(x＋14)＝5(2x−14) 　−3x＝−168で,x＝56 これをウに代入して, 　y＝2×56＝112 よって,56＋112＝168人 ７(右図参照) イ,エ 　ア x＜0ではｙは減少 　ウ 原点を通るから,0≦y≦4 ８ 順に並べ直すと, 　18，20，23，25，26，26だから, 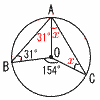　中央値＝(23＋25)÷2＝24ｍ ９(右図参照) 　△OAB,△OACは二等辺三角形 　∠BAC＝x＋31＝154÷2より, 　x＝77−31＝46°
20長野県	１ 3＋5＝8 ２ ウ ３ 2で割って,x−1＝−3より,x＝−2 ４ 5√3− 　9√3 . ＝5√3−3√3＝2√3 √3√3 ５ 2nは常に偶数だから,奇数はウ,エ ６ あ 700　　い 2 ７ y＝に(2,−8)を代入すると, 　−8＝より,a＝−16 　y＝−にx＝3を代入して,y＝− ８ 原点が最小値 　x＝−1のとき,y＝2×(−1)2＝2 　x＝0のとき,y＝2×02＝0 　x＝2のとき,y＝2×22＝8 　　0≦y≦8で,ア ９（右図参照） 　110円以上は3通り 　確率＝ 10 右図 　線分BDまたはACの 　　垂直二等分線を引く 11 (1) 中点連結定理より, 　　　AC//MNで, 　∠BMN＝80°(錯角) (2) （右図参照） 　四角形AMPCは 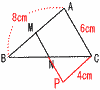　　　平行四辺形 　PC＝AM＝4cm 周の長さ＝(4＋6)×2 　　＝20cm	24三重県	【　前　期　】 １ 9−10＝−1 ２ 　5(4x−3)−2(6x−7) ＝ 8x−1 　2×5 10 ３ 16x2y2×(−3x)＝−48x3y2 ４ 上式×3＋下式より, 　17x＝−34で,x＝−2 　これを下式に代入して, 　　5×(−2)＋9y＝−13 　　9y＝−13＋10で,y＝− 　よって,x＝−2,y＝− ５ 5√6＋2・2√6− 6√3・√2 √2・√2 　＝5√6＋4√6−3√6＝6√6 ６ x2−2x−24＝6x−39 　移項して整理すると,x2−8x＋15＝0 　(x−3)(x−5)＝0より,x＝3,5 ７ 　x＝−5のとき,y＝a×(−5)2＝25a 　x＝−3のとき、,y＝a×(−3)2＝9a 変化の割合＝ 　9a−25a . ＝ −16a ＝−8a＝2 (−3)−(−5) 2 　よって,a＝− ８ ×52π×6＝50πcm3 ９ 〇をx,●をyとすると, 　△ABCで,2x＋40＝2yより,x＝y−20 　△EBCで,x＋∠E＝yより, 　　∠E＝y−x＝y−(y−20)＝20° 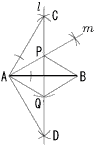10 右図 ・線分ABの垂直二等分線l を引く ・△ABCが正三角形となる 　　ような点Cをとる ・△ABDが正三角形となる 　　ような点Dをとる ・∠CABの二等分線mを引く ・l とmの交点をPとする ・AP＝AQとなる点Qをl 上にとる ・4点A,Q,B,Pを結ぶ
21岐阜県	１ 9−2＝7 ２ 2y＝6−4xで,y＝3−2x ３ 3√3＋√3−2√3＝2√3 ４ x＝2のとき,y＝2×22＝8 　 x＝5のとき,y＝2×52＝50 　変化の割合＝ 50−8 ＝14 5−2 ５ 2けたの整数は全部で,5×4＝20通り 　2枚目は偶数で,2通り, 　1枚目は2枚目以外の4通り, 確率＝ 4×2 ＝ 2 20 5 ６ 直径をそれぞれx,yとすると, 　太線＝xπ＋yπ＝(x＋y)π 　x＋y＝10だから, 　　太線＝×10π＝5πcm 　〜２番問題（おまけ）〜 １ 9人の階級で,(20＋25)÷2＝22.5分 ２ 15分未満は,4＋10＋16＝30人 　30÷100＝0.3 ３ イとエ ア Bの最頻値は17.5分　× イ Aは17.5分,Bは17.5分　〇 ウ Aは0.33　× エ Aは25分,Bは35分　〇		【　後　期　】 １ −63 ２ 　16x−15x ＝ x 　5×4 ３ 7a−7b−8a＋32b＝−a＋25b ４ 5−2√10＋2＝7−2√10 ５ (x−6)(x＋6) ６ 解の公式より, 　x＝ −5±√52−4×1×(−1) 2×1 　　＝ −5±√25＋4 ＝ −5±√29 2 2 ７ 5＋4＋3＋7＋n＋5＝5.5×6 　n＋24＝33より、n＝9