全国公立高校入試 　１番問題　【令和２年春】	正　答　２
	９　栃木県　〜　16　富山県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

９栃木県	１ −9 ２ 4x＋4y−6x+3y＝−2x＋7y ３ 　a2×(−4)ab2 ＝− a3b2  6 ４ 5√2√3×√3＝5√2×3＝15√2 ５ x2−64 ６ 元の方程式にx＝7を代入すると, 　2×7−a＝−7＋5 　−a＝−2−14より,a＝16 ７　6x＋y＝100　（100−6x＝yも可） ８ ABは直径だから,∠ACB＝90° 　OA＝OCより,∠OCA＝39° 　∠x＝90−39＝51° ９ x(x−9)＝0より,x＝0,9 10 　　9＋3　. ＝ 12 ＝ 6 　9＋2＋3 14 7 　（1−2/14＝も可） 11 円柱＝32π×6＝54πcm3 12 x:4＝2:5より,5x＝8で,x＝(1.6も可) 13 ウ 　グラフより,傾きa＜0,切片b＞0 14 不良品がx個とすると, 　比率より, 2 ＝ 　x　. で, 100 4500 　x＝2×4500÷100＝90個	13東京都	１ 9−16＝−7 ２ 15a−3b−7a＋4b＝8a＋b ３ 2＋2√6−√6−6＝−4＋√6 ４ 移項して,9x−5x＝40−4 　4x＝36より,x＝9 ５ 上式＋下式×3より,10y＝30で,y＝3 これを下式に代入して,x＋3＝8で,x＝5 よって,x＝5,y＝3 ６ 解の公式より, 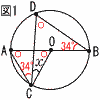　x＝ −9±√92−4×3×5 2×3 　　＝ −9±√81−60 ＝ −9±√21 6 6  ７ 15分未満は、12＋14＝26人 　26÷40×100＝65(％) ８(右図参照) ∠AOC＝∠BDC(仮定)、 ∠BAC＝∠BDC(対頂角) ∠BAC＝∠OCA(底角)だから, 　△OACは正三角形 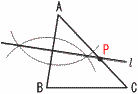∠x＝60−34＝26° ９ 右図 ・辺ABの垂直二等分線l を引く ・l と辺ACの交点をPとする
10群馬県	【前期】 １ (1) −4−5＝−9　(2) −21ａ　 　(3) 5x＋10−2x−8＝3x＋2 　(4) 　2(x＋y）−(x＋3y) ＝ x−y 　6 6 　(5) 8a2b÷4a2＝2b 　(6) 　10×√5 −3√5＝2√5−3√5 　√5√5 　　＝−√5 ２ 2xy(x−2y) ３ 90−4a×b＝90−4ab(cm) ４ y＝に(2,−6)を代入すると, 　−6＝で,a＝−12 　よって,y＝− ５ x2−2x−3＝0 　(x−3)(x＋1)＝0より,x＝3,−1 ６ AC＝√22＋42＝√20＝2√5cm ７ ∠C＝∠B＝85° 　∠BDC＝138−85＝53°	14神奈川県	ア 2＋9＝11 (答４) イ −13ab (答２) ウ 2√7＋７√7＝9√7 (答２) エ 　4(3x−y)−3(x−2y) ＝ 9x＋2y (答４) 12 12 オ √2＋1＝Ａとおくと、 　与式＝A2−5A＋4＝(Aー1)(A−4) 　＝(√2＋1−1)(√2＋1−4)＝√2(√2−3) 　＝2−3√2 (答１) 　〜２番問題（おまけ）〜 ア 元の式に(2,1)を代入すると, 　{ 2a＋b＝10 で,これを解いて, 2b−a＝5 　a＝3,b＝4 (答２) イ 解の公式より, 　x＝ −(−5)±√(−5)2−4×1×(−3) 2×1 　　＝ 5±√25＋12 ＝ 5±√37  (答４) 2 2 ウ 変化の割合＝ (−×62)−(−×32) 6−3 　＝ −12＋3 ＝−3 (答２) 3 エ 子どもの入園料をx円とすると, 　(x＋600):x＝5:2より,2(x＋600)＝5x 　3x＝1200で,x＝400円 (答１) オ 5880＝23×3×5×72だから, 　n＝2×3×5＝30 (答３) 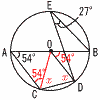カ(右図参照) 　∠BAD＝∠BED×2＝54° 　∠OAC＝∠OCA＝54° 　∠ODC＝∠OCD＝xとすると, 四角形OACDで, 　2x＋54×2＋(180−54)＝360 　2x＝360−234より,x＝63°(答２)
	【後期】 １ (1) 1−8＝−7　(2) x　(3) 4ab2 ２ イ 3.5　ウ 約2.8　エ 約3.3 で, イ ３ (x−5)2 ４ 上式＋下式×2より,5y＝10で,y＝2 　これを下式に代入すると、 　　−x＋2＝3より、x＝−1 　よって,x＝−1,y＝2 ５ (1回は表)の確率＝1−(全て裏)の確率 　＝1−()3＝1−＝ ６ 2x−5＝±√18＝±3√2 　x＝ 5±3√2 2 ７ BDは直径だから,∠BCD＝90° 　　∠BAC＝∠BDC＝90−38＝52° ８ 黒いビーズをx個とすると, 　白の比率＝ 　100 . ＝ 10 より、 x＋100 100 　10(x＋100）＝100×100 　x＝900で,ウ ９ ∠cと∠e
11埼玉県	１ 2x　２ 10＋3＝13　３ 4x2 ４ 3x＝3より,x＝1 ５ 3√2−6√2＝−3√2 ６ (x＋6)(x−2) ７ 上式−下式×2より, 　−y＋4y＝1＋14で,y＝5 　これを上式に代入して, 　　6x−5＝1より,x＝1 　よって,x＝1,y＝5 ８ 解の公式より, 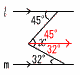　x＝ −(−5)±√(−5)2−4×3×1 2×3 　　＝ 5±√25−12 ＝ 5±√13 6 6 ９(右図参照) ∠xの頂点から平行線を引く 　∠x＝45＋32＝77° 10 変化の割合 　＝ 2×42−2×22 ＝12 4−2 11 平行でない, 交わらない辺で、エ 12 ウ 13 高さをh,体積をVとすると, 　h2＋32＝52より,h＝√25−9＝4 　V＝×32π×4＝12π よって,高さ4cm, 体積12πcm3 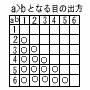14(右表参照) 表より15通りで, 　確率＝ 15 ＝ 5 36 12 １５ 平均値＝(5+4+7+5+9)÷5 　＝30÷5＝6回 少ない順に並べると, 4,5,5,7,9だから, 中央値は3人目で,5回 １６ イ 　母集団(全校生徒))から無作為(乱数さい)に選んでいるから	15新潟県	１ 14−9＝5 ２ 15a＋3b＋7a−4b＝22a−b ３ 　6a2b×ab ＝3a3 　2b2 ４ 上式×2−下式より,−7y＝14で,y＝−2 　これを上式に代入して,x−4×(−2)＝9 　　x＝9−8＝1 　よって, x＝1,y＝−2 ５ √8−√2＝2√2−√2＝√2 ６ 解の公式より, 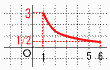　x＝ −3±√32−4×1×(−1) 2×3 　　＝ −3±√9＋4 ＝ −3±√13 2 2  ７ (右図参照) 　x＝1のとき,y＝3/1＝3 　x＝6のとき,y＝3/6＝ 　よって,≦y≦3 ８ △AED∽△CEB(相似比は2:5)より, 　　　DE:BE＝2:5だから、DE:DB＝2:7 　 △DEF∽△DBC(相似比は2:7)より, 　　 EF:BC＝2:7だから、EF:5＝2:7で, 　　 EF＝5×2÷7＝10/7cm 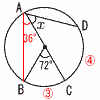９ (右図参照) AとBを結ぶ 　∠BAC＝72÷2＝36° 　x：36＝4：3より, 　　x＝36×4÷3＝48° 10 青色の玉をx個とすると, 　青玉の比率＝ 　x . ＝ 7 より, 480 40 　x＝480×7÷40＝84個
12千葉県	【前期】 １ 7 ２ −25＋18×＝−25＋12＝−13 ３ 2x＋8y−x＋y＝x＋9y ４ 両辺×3より, 　3x−21＝4x−9 　−x＝12で,x＝−12 ５ 5√2＋6√2− 14×√2 √2√2 　＝11√2−7√2＝4√2 ６ 2(x2−16)＝2(x＋4)(x−4) 【後期】 １ −18 ２ 9−16×＝9−10＝−1 ３ 　a2b×21b ＝3ab2 　7a ４ 上式×10−下式×2より, 　15y−(−6)y＝40−(−2) 　21y＝42で,y＝2 　これを下式に代入して, 　　x−3×2＝−1で,x＝5 よって,x＝5,y＝2 ５ 　12√3 . −3√6×2√2＝4√3−6√12 √3√3 　＝4√3−12√3＝−8√3 ６ 解の公式より, 　x＝ −5±√52−4×1×5 1×2 　　＝ −5±√25−20 ＝ −5±√5 2 2	16富山県	１ 5−6＝−1 ２ 　3xy2×4y ＝− 6y2 　−2x2y x ３ 3√5＋√5−2√5＝2√5 ４ 与式＝(a＋2)(a−2)＝a2−4＝(√6)2−4＝2 ５ 下式×2−上式より,x＝5 　これを下式に代入して,2×5＋y＝6で,y＝−4 　よって, x＝5,y＝−4 ６ (x＋8)(x−2)＝0より, x＝−8,2 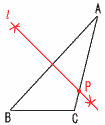７ 1500(1− a )＝(1500−150a)円 10 ８ 右図 ・線分ABの 　　　垂直二等分線l を引く ・l とACの交点にPをとる ９（下図参照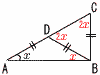） 　△DABで,∠A＝∠DBA＝x 　△BCDで,∠C＝BDC＝2x 　∠A＋∠C＝x＋2x＝3x＝90°より,∠x＝30° 10 12人の7.0〜7.5秒の階級だから, 　(7.5−7.0)÷2＝7.25秒