全国公立高校入試 　１番問題　【令和２年春】	正　答　１
	１　北海道　〜　８　茨城県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

１北海道	１ (1) −15 　(2) 9−36＝−27 　(3) (√2・√7)×√7−2√2＝7√2−2√2 　　　　＝5√2 ２ −4,4　（±4も可） ３ 資料を気温の高さ順に並べかえると, 　21.2， 22.2， 24.2， 25.9， 31.1， 　32.0， 34.2 　中央値は4番目で,25.9℃ ４ ねじれの位置とは, 　　平行でない,交わらないものだから辺OC ５ y＝axに(2,−6)を代入して, 　　−6＝2aより,a＝−3(比例定数) 　y＝−3xにx＝−3を代入すると, 　　y＝−3×(−3)＝9 ６ 線分ABは直径だから, 　　その円周角の∠C＝90° 　△ABCは直角三角形になるから, 　　三平方の定理より,AC2＋22＝52 　　AC2＝25−4＝21で,AC＝√21cm	４岩手県	１ −3　　２ 2(2a＋1)＝4a＋2 ３ 7−1−6 ４ 上式ー下式より,x＋6＝−2x＋3 　3x＝−3で,x＝−1 　これを上式に代入して, 　　y＝−1＋6＝5 　よって,x＝−1,y＝5 ５ 解の公式より, 　x＝ −(−3)±√(−3)2−4×1×(−2) 2×1 　　＝ 3±√9＋8 ＝ 3±√17 2 2 　〜　２番問題（おまけ）　〜 　y＝4x, ア 　〜　３番問題（おまけ）　〜 （答） 団体Ｘ （理由） 団体Ｘは34a円,団体Ｙは40a×0.8＝32a円 　34a＞32aより,団体Ｘの方が多くかかる
２青森県	１ ア −5＋7＝2　 　イ ×12−×12＝3−8＝−5 　　（ 3−8 ×12＝ −5 ×12＝−5も可） 12 12 　ウ . 4x×2xy ＝ 8x2y ＝y 5×2x2 10x2 　エ (−4a2＋9)＋9＝−4a2＋18 　オ √3−2√3＝−√3 　2）150 　3） 75 　5） 25 　5）　5 　　　 1 . ２ 100a＋50b＝10c ３ (右の計算参照) 2×3×52 ４ 上式を下式に代入すると, 　6x−4(x＋2)＝−10 　2x＝−2より,x＝−1 　これを上式に代入して, 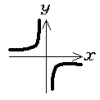　　y＝4(−1＋2)＝4 　よって,x＝−1,y＝4 ５ グラフは右図 　エ ６ 白玉がx個とすると, 　黒玉の割合 ＝ 　100　. ＝ 4 x＋100 34 　4(x＋100)＝100×34 　4x＝3400−400で,x＝750個 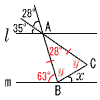７ (右図参照) 2y＋28＝180より,y＝76° ∠x＝180−63−76＝41° ８ 底面積も忘れずに！ 表面積＝側面積＋底面積 　＝4π×62÷2＋62π＝108πcm2	５山形県	１ (1) −3＋2＝−1 　(2) −×＋×＝−＋＝ 　(3) 　9ａ2×(−16ａｂ2) ＝−24a2b 　6ａｂ 　(4) 3＋6√3＋5−4√3＝8＋2√3 ２ 2x2−8x−x＋4＝−4x＋2 　　2x2−5x＋2＝0 　　(2x−1)(x−2)＝0 　2x−1＝0 または, x−2＝0 　よって, x＝, 2 [別解] 　　2x2−5x＋2＝0 解の公式より, 　x＝ −(−5)±√(−5)2−4×2×2 2×2 　　＝ 5±√25−16 ＝ 5±√9 ＝ 5±3 2 2 2 　よって, x＝, 2 ３ 少なくとも１個は白玉 　　　＝1−(すべて赤玉)　と考える 確率＝1−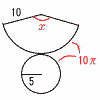××＝1−＝ ４（右図参照） 扇形の弧＝底面の円周＝10πcm 20π×＝10πより、x＝180° よって, ウ ５ エ 7時間〜9時間の割合は, 　1組が,21/32≒0.65 　2組が,21/33≒0.63
３秋田県	【前期】 １ 5＋21＝26 ２ 4√3＋5√3−2√3＝7√3 ３ 　3x−2(2x−y) ＝ −x＋2y 　6 6 ４ (a−b)(x−y) ５ 上式＝下式より,x−2＝−3x＋14 　4x＝16で,x＝4 これを上式に代入して,y＝4−2＝2 　よって,x＝4,y＝2 ６ 解の公式より, x＝−(−2)±√(−2)2−1×2＝2±√2 ７ x:6＝(9＋4):4より,4x＝78 　　x＝19.5　（x＝39/2も可）	６宮城県	１ −5 ２ −×＝−18/25 ３ 与式＝12x＋3y−12x＋2＝3y＋2 ４ 　6a2b×2b ＝4ab 　3ab ５ 4√2−3√2＋√2＝2√2 ６ (x＋3)(x−8)＝0より,x＝−3,8 ７ ウ,オ 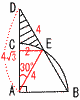８(右図参照) △EDA＝×4√3×2＝4√3 扇形ACE＝42π×(30/360)＝π 斜線部＝4√3−π(cm2)
	【後期】 １ 1−0.4＝0.6　（も可） ２ 　6×√2 ＝ 6√2 ＝3√2 　√2√2 2 ３ 与式＝3a−6b−15a＋5b＝−12a−b 　　＝(−12)×−3＝−6−3＝−9 ４ 3a＋2b≧20 ５ 両辺×3より, 　2x＋4＝12で,x＝4 ６ 下式を上式に代入して, 　2(−5y＋4)−3y＝−5 　−13y＝−13で,y＝1 これを下式に代入して,x＝−5×1＋4＝−1 　よって,x＝−14,y＝1 ７ x＝−1を元の方程式に代入すると, 　(−1)2−2a×(−1)＋3＝0 　1＋2a＋3＝0より,a＝−2 　これを元の方程式に代入して, 　　x2−2(−2)x＋3＝0 　　x2＋4x＋3＝0 　　(x−3)(x＋1)＝0より,x＝3 ８ 行きの時間＝ a 分，帰りの時間＝ a 分 60 90 平均速度＝2a÷( a ＋ a )＝2a÷ 3a＋2a 60 90 180 　＝分速72m ９ ア ア すべての内角が等しい三角形は正三角形はである。(〇) イ 対角線がそれぞれの中点で交わる四角形は長方形である。(×) ウ x＞4ならば x≧5である。(×) エ x2＝1ならば x＝1 である。(×) 10 √120＋a2＝xとすると,x2−a2＝120 　(x＋a)(x−a)＝120で,x＋a＞x−a＞0 　　かつ,x＋aとx−aは偶奇が一致 (x＋a,x−a)＝(60,2)(30,4)(20,6)(12,10)で, 　a＝1,7,17,29のとき,4個 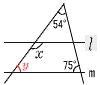11（右図参照） ∠y＝180−54−75＝61° ∠x＝180−61＝119° 12 外角の和は360°だから, ∠xの外角＝180−(55＋115＋65＋79)＝314 よって,∠x＝360−314＝46° 13 ねじれの位置とは, 　　平行でない,交わらないものだから, 　HI,IJ,KL,LG,CI,DJ,EK,FLで, 8本 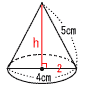14(右図参照) 　h＝√52−22＝√21cm 体積＝×22π×√21 　＝√21πcm3 15 対応する辺の比が BA ＝ 5 × BC ＝ 2 × BD ＝ 2 だから、 BR 4 BP 1 BQ 1 　×2×2＝5倍	７福島県	１(1) −6 　(2) (−12)×＝−9 　(3) 6x−3y−x＋5ｙ＝5x＋2y 　(4) 2√5＋√5＝3√5 ２ y＝axに(3,−15)を代入すると, 　−15＝3aで,a＝−5 　よって,y＝−5x 　〜２番問題（おまけ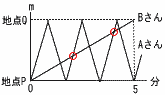）〜 １ イ ２ a÷1.25＝a÷ 　　＝a(個) 　（0.8aも可） ３(右上図の赤丸参照) 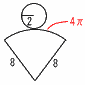すれ違いの場合は除くから,2回 ４(右図参照) 扇形の弧＝底面の円周＝4πだから, 　側面積＝×4π×8＝1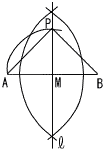6πcm2 ５ 右下図 ・線分ABの垂直二等分線l 　　を引く ・ABとの交点(中点)Mをとる ・MA＝MPとなる点Pをl 上に 　　とる ・PAとPBを引く
		８茨城県	１ −3−(＋2)＝−5℃ ２ 1辺の長さをxとすると,x2＝50 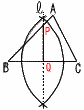　x＝√50＝5√2cm ３ ア ４ 右図 ・辺BCの垂直二等分線l を引く ・l とABの交点Pをとる ・l とBCの交点Qをとる ・折り目は線分PQ 　〜２番問題（おまけ）〜 １ ア 100a＋10b＋5　　イ 20a＋2b＋1 ２ ア x＋y　　イ 0.8x＋y−800