|
(42)長崎県 | 学習日 月 日( ) |
|
(42)長崎県 | 学習日 月 日( ) |
| 【 A 】 | |||
| 1 | 8 | 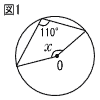 図1のような円Oにおいて,∠xの大きさを求めよ。 図1のような円Oにおいて,∠xの大きさを求めよ。 |
|
| 2 | |||
| 3 | 3√5−√80 |
9 | 箱の中に同じ大きさの赤玉と白玉が合わせて500個入っている。この箱の中の玉をよくかき混ぜてから30個の玉を無作為に抽出すると,赤玉24個,白玉6個がふくまれていた。 はじめに箱の中に入っていた白玉の個数はおよそ何個と考えられるか。 |
| 4 | 本体価格(税抜価格)980円の商品を1つだけ購入する。10%の消費税がかかるとき,支払う金額(税込価格)を求めよ。 |
||
| 5 | ある科学館の入館料は,おとな1人a円,子ども1人b円である。おとな3人と子ども4人の入館料の合計は3000円より安い。この数量の間の関係を不等式で表せ。 |
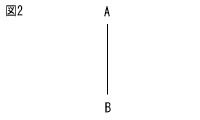
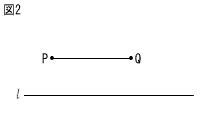
10 | 図2において,線分ABの垂直二等分線を定規とコンパスを用いて解答用紙の図2に作図せよ。ただし,作図に用いた線は消さずに残しておくこと。 |
| 6 | a(x+y)+2(x+y) を因数分解せよ。 |
 |
|
| 7 | 2次方程式 x2−3x−2=0 を解け。 |
||
| 【 B 】 | ||||||||||
| 1 |
|
6 |
|
|||||||
| 2 | ある科学館の入館料は,おとな1人a円,子ども1人b円である。おとな3人と子ども4人の入館料の合計は3000円より安い。この数量の間の関係を不等式で表せ。 |
|||||||||
| 3 | (x+y)2+7(x+y)+12 を因数分解せよ。 |
7 |  図1のような円Oにおいて,∠xの大きさを求めよ。 図1のような円Oにおいて,∠xの大きさを求めよ。 |
|||||||
| 4 | 2次方程式 (x−2)(x+3)=−2x を解け。 |
8 | ただし,作図に用いた線は消さずに残しておくこと。 |
|||||||
| 5 | 箱の中に赤玉だけがたくさん入っている。その箱の中に,赤玉と同じ大きさの白玉100個を入れ,よくかき混ぜた後,その中から20個の玉を無作為に抽出すると,白玉がちょうど4個ふくまれていた。はじめに箱の中に入っていた赤玉の個数はおよそ何個と考えられるか。 |
 |
||||||||
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] [答のペ−ジに進む] |